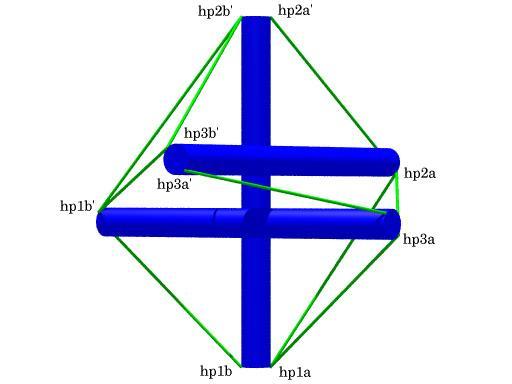
View of the Tensegrity Prism
with Point Labels
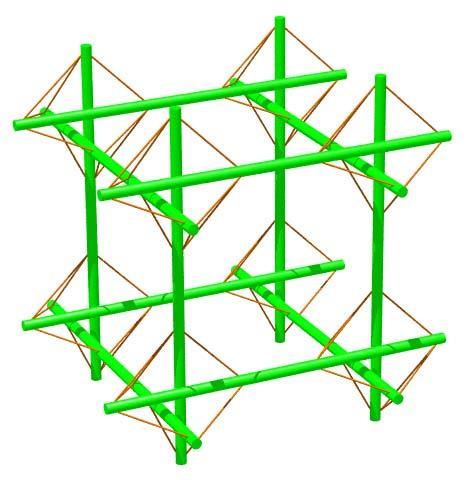
Cell of Cubic Lattice Constructed using
Tensegrity Prisms as Joints
structure file: tprism/x3prism_orthoj2.rc variable file: tprism/x3prism_orthoj2.dat digit list: src/standard.dls |
Hub Connectivity
This shows how vectors (v1, v2, v3) are applied to the
strut end points (p1, p1', p2, p2', p3, p3') to derive
hub points (hp1a, hp1b, ...). Hub points are where tendons
are connected to the strut.
<VecPt> hp1a p1 + v1
<VecPt> hp1b p1 - v1
<VecPt> hp1a' p1' + v3
<VecPt> hp1b' p1' - v3
<VecPt> hp2a p2 + v2
<VecPt> hp2b p2 - v2
<VecPt> hp2a' p2' + v1
<VecPt> hp2b' p2' - v1
<VecPt> hp3a p3 + v3
<VecPt> hp3b p3 - v3
<VecPt> hp3a' p3' + v2
<VecPt> hp3b' p3' - v2
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
This figure was computed without benefit of symmetry transforms,
but everything turned out very symmetric nevertheless.
# struts
<Member> strut1 p2' p1 -1.0 sqr(12.0) 1 Con CalcClear *
<Member> strut2 p3' p2 -1.0 sqr(12.0) 1 Con CalcClear *
<Member> strut3 p1' p3 -1.0 sqr(12.0) 1 Con CalcClear *
# side tendons
<Member> side1 hp1a' hp1b 1.0 0.0 3 Obj CalcClear *
<Member> side2 hp2a' hp2b 1.0 0.0 3 Obj CalcClear *
<Member> side3 hp3a' hp3b 1.0 0.0 3 Obj CalcClear *
# end tendons
<Member> end1 hp2a hp1a 1.0 sqr(8.38288) 2 Con CalcClear *
<Member> end2 hp3a hp2a 1.0 sqr(8.38288) 2 Con CalcClear *
<Member> end3 hp1a hp3a 1.0 sqr(8.38288) 2 Con CalcClear *
<Member> end1' hp2b' hp1b' 1.0 sqr(8.38288) 4 Con CalcClear *
<Member> end2' hp3b' hp2b' 1.0 sqr(8.38288) 4 Con CalcClear *
<Member> end3' hp1b' hp3b' 1.0 sqr(8.38288) 4 Con CalcClear *
Hub Constructs
These items are just vectors corresponding to each of the
struts. At some point the software will be modified so
these items aren't necessary since it should be possible
to treat any member as a vector without explicit constructs.
<DiffVec> strut1v p2' p1
<DiffVec> strut2v p3' p2
<DiffVec> strut3v p1' p3
Hub Constraints
These are constraints the hub vectors must meet. Each
vector must be orthogonal to its strut and 0.5 inches long.
<VecDotVec> hubdot1 strut1v v1 1.0 0.0 Con
<VecLength> hublength1 v1 1.0 sqr(0.5) Con
<VecDotVec> hubdot2 strut2v v2 1.0 0.0 Con
<VecLength> hublength2 v2 1.0 sqr(0.5) Con
<VecDotVec> hubdot3 strut3v v3 1.0 0.0 Con
<VecLength> hublength3 v3 1.0 sqr(0.5) Con
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. These are raw unadjusted values and
assume the hubs of the structure are single points. The
values are in model units.
strut1: 12 strut2: 12 strut3: 12
side1: 6.65617 side2: 6.65617 side3: 6.65617
end1: 8.38288 end2: 8.38288 end3: 8.38288
end1': 8.38288 end2': 8.38288 end3': 8.38288
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
strut1: -10.4407 strut2: -10.4407 strut3: -10.4407
side1: 6.65617 side2: 6.65617 side3: 6.65617
end1: 4.33197 end2: 4.33197 end3: 4.33197
end1': 4.33197 end2': 4.33197 end3': 4.33197
Construction Lengths
(stakes and #18 twisted nylon twine (white) --
inches, 16ths and 32nds)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for a strut
represents the distance between tendon attachment points
on the strut assuming both attachment points are on the same
side of the strut. Prestress forces are assumed to affect
tendon lengths and not strut lengths. For this particular hub
geometry, the ad hoc adjustment used in the first datasheet
didn't work very well. Here no ad hoc adjustment is necessary
since the hubs are included explicitly in the mathematical
programming problem. The struts were cut from
1-inch by 1-inch hardwood garden stakes. The behavior
of the #18 twisted nylon twine under stress is highly non-linear,
so a look-up table was used to compute strains.
stress-strain chart: v04oct_d/wellingtn.ssc
Average Tendon Force Magnitude (chart units)> 20
Length Scale Factor> 1.0
(Things are scaled so model and construction units are the same.)
Strut and Tendon Hub Adjustments - s;t> 0 0
(As seen above, hub connections were handled explicity in
the mathematical programming problem, so no ad hoc
adjustment is needed here to account for the hub connections.)
strut1: 12 0 0 strut2: 12 0 0 strut3: 12 0 0
side1: 6 0 0 side2: 6 0 0 side3: 6 0 0
end1: 7 12 0 end2: 7 12 0 end3: 7 12 0
end1': 7 12 0 end2': 7 12 0 end3': 7 12 0
Alternate Construction Lengths
(stakes and #1 braided nylon twine (yellow) --
inches, 16ths and 32nds)
For my version of the structure, I tied half the prisms (4)
with this twine, and half with the twisted twine. This
twine looks nicer and doesn't unravel like the twisted.
This twine is also more elastic which is why the construction
lengths are shorter. When used at the same tensions,
as I do here, the mechanical properties of the braided twine
seem equivalent to the white nylon twine.. The braided
twine's behavior under stress is different from the
behavior of twisted twine, so a different look-up table
was used to compute strains.
stress-strain chart: v02oct_s/evans.ssc
Average Tendon Force Magnitude (chart units)> 20
Length Scale Factor> 1.0
Strut and Tendon Hub Adjustments - s;t> 0 0
strut1: 12 0 0 strut2: 12 0 0 strut3: 12 0 0
side1: 5 13 1 side2: 5 13 1 side3: 5 13 1
end1: 7 9 0 end2: 7 9 0 end3: 7 9 0
end1': 7 9 0 end2': 7 9 0 end3': 7 9 0

View of the Tensegrity Prism
with Point Labels

Cell of Cubic Lattice Constructed using
Tensegrity Prisms as Joints
structure file: tprism/x3prism_orthoj2.rc variable file: tprism/x3prism_orthoj2.dat digit list: src/standard.dls |
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com