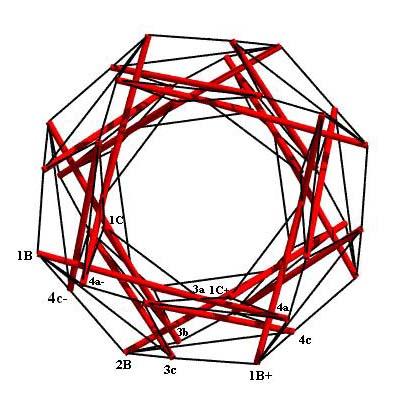
Axial View of the Eight-Stage Tensegrity Torus
with Point Labels
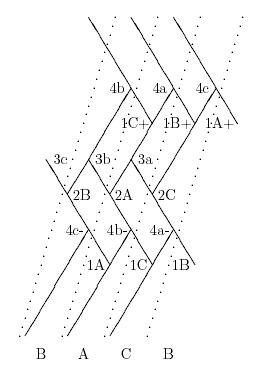
Schematic for the Tensegrity Torus
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
<Member> st13a pt1A pt3c 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> st24a pt2A pt4a 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> guy1a pt1A pt3b 1.00 0.0 3 Obj *
<Member> guy2a pt2A pt4b 1.00 + 0.493154 0.0 3 Obj *
<Member> TS23a pt2A pt3a 0.0 sqr(1.0) 2 Con *
<Member> tS23a pt2A pt3b 0.0 sqr(1.0) 2 Con *
<Member> tT31a pt3a pt1C+ 2.00 + 0.493154 0.0 3 Obj *
<Member> tT42a pt4a- pt2C 2.00 0.0 3 Obj *
<Member> TS41a pt4a pt1B+ 0.0 sqr(1.0) 2 Con *
<Member> tS41a pt4a pt1C+ 0.0 sqr(1.0) 2 Con *
<Member> st13b pt1B pt3a 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> st24b pt2B pt4b 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> guy1b pt1B pt3c 1.00 - 0.493154 0.0 3 Obj *
<Member> guy2b pt2B pt4c 1.00 - 0.493154 0.0 3 Obj *
<Member> TS23b pt2B pt3b 0.0 sqr(1.0) 2 Con *
<Member> tS23b pt2B pt3c 0.0 sqr(1.0) 2 Con *
<Member> tT31b pt3b pt1A+ 2.00 0.0 3 Obj *
<Member> tT42b pt4b- pt2A 2.00 + 0.493154 0.0 3 Obj *
<Member> TS41b pt4b pt1C+ 0.0 sqr(1.0) 2 Con *
<Member> tS41b pt4b pt1A+ 0.0 sqr(1.0) 2 Con *
<Member> st13c pt1C pt3b 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> st24c pt2C pt4c 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> guy1c pt1C pt3a 1.00 + 0.493154 0.0 3 Obj *
<Member> guy2c pt2C pt4a 1.00 0.0 3 Obj *
<Member> TS23c pt2C pt3c 0.0 sqr(1.0) 2 Con *
<Member> tS23c pt2C pt3a 0.0 sqr(1.0) 2 Con *
<Member> tT31c pt3c pt1B+ 2.00 - 0.493154 0.0 3 Obj *
<Member> tT42c pt4c- pt2B 2.00 - 0.493154 0.0 3 Obj *
<Member> TS41c pt4c pt1A+ 0.0 sqr(1.0) 2 Con *
<Member> tS41c pt4c pt1B+ 0.0 sqr(1.0) 2 Con *
Rotation Matrices
Only part of the structure is specified using the members
above. The rest is generated using symmetry transformations.
Here the first symmetry transformation is specified as a 3x3
pre-multiplication matrix in row-major format. Others are
constructed by multiplying the first one by itself. As with
the members, the first item is always the label used for
the transform.
<XMat> x1 cos(2*pi/4) (-sin(2*pi/4)) 0 sin(2*pi/4) cos(2*pi/4) 0 0 0 1
<CompositeXform> x2 x1 x1
<CompositeXform> x3 x1 x2
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
screw-eye center to screw-eye center, as are the tendon lengths.
These values are in model units.
st13a: 2.5 st24a: 2.5 guy1a: 2.01029
guy2a: 1.54864 TS23a: 1 tS23a: 1
tT31a: 0.628066 tT42a: 1.06676 TS41a: 1
tS41a: 1 st13b: 2.5 st24b: 2.5
guy1b: 2.51316 guy2b: 2.51316 TS23b: 1
tS23b: 1 tT31b: 1.06676 tT42b: 0.628066
TS41b: 1 tS41b: 1 st13c: 2.5
st24c: 2.5 guy1c: 1.54864 guy2c: 2.01029
TS23c: 1 tS23c: 1 tT31c: 1.41420
tT42c: 1.41420 TS41c: 1 tS41c: 1
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
st13a: -3.19754 st24a: -5.55701 guy1a: 2.01029
guy2a: 2.31236 TS23a: 3.50881 tS23a: 2.62149
tT31a: 1.56587 tT42a: 2.13352 TS41a: 2.94064
tS41a: 2.62149 st13b: -4.80177 st24b: -4.80177
guy1b: 1.27378 guy2b: 1.27378 TS23b: 2.94064
tS23b: 2.91878 tT31b: 2.13352 tT42b: 1.56587
TS41b: 3.50881 tS41b: 2.59506 st13c: -5.55701
st24c: -3.19754 guy1c: 2.31236 guy2c: 2.01029
TS23c: 2.20944 tS23c: 2.59506 tT31c: 2.13099
tT42c: 2.13099 TS41c: 2.20944 tS41c: 2.91878
Average tendon force magnitude: 2.35175
Worst-Case Clearances in Model Units
These clearances are measured from member centerline to
member centerline. The labels of the two members are specified
as well as a transformation for the second member. If "id"
is specified for the transformation, it means none was applied.
0.236335 st24a st24b id
0.236335 st13b st13c id
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of a 5/16-inch-diameter wooden dowel.
The tendons can be made of braided nylon fishing line.
Prestress forces were assumed not to affect strut lengths.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 290/2.5
Strut and Tendon Hub Adjustments - s;t> 5 3.5
(The 5 mm adjustment for the strut is the amount
the screw-eye center extends from the dowel. The 3.5 mm
adjustment for the tendon is half the outer diameter of the
screw eye.)
st13a: 280 0 st24a: 280 0 guy1a: 222 1 guy2a: 169 1
TS23a: 106 0 tS23a: 106 1 tT31a: 65 0 tT42a: 114 1
TS41a: 106 1 tS41a: 106 1 st13b: 280 0 st24b: 280 0
guy1b: 281 1 guy2b: 281 1 TS23b: 106 1 tS23b: 106 1
tT31b: 114 1 tT42b: 65 0 TS41b: 106 0 tS41b: 106 1
st13c: 280 0 st24c: 280 0 guy1c: 169 1 guy2c: 222 1
TS23c: 107 0 tS23c: 106 1 tT31c: 154 1 tT42c: 154 1
TS41c: 107 0 tS41c: 106 1

Axial View of the Eight-Stage Tensegrity Torus
with Point Labels

Schematic for the Tensegrity Torus
structure file: torus/x3l08torus1.rc
variable file: torus/x3l08torus1.dat
digit list: src/mm.dls
|
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com