
After designing the X-Module Double Helix, I got interested in building a tensegrity torus with same-sense X-Modules instead of the alternating sense modules I'd used before. I was curious how the not-quite-three period of the double helix would translate into a torus. In addition, using same-sense modules allowed the building of a torus with an odd number of stages instead of the even number of stages which using alternating-sense modules constrains one to.
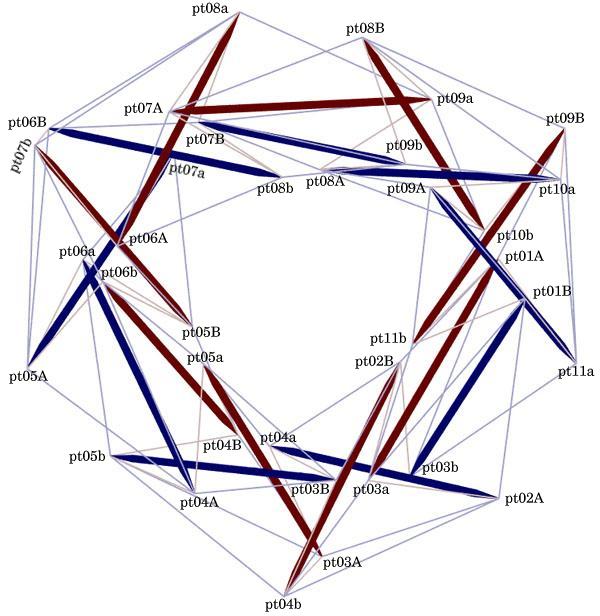
The result is the design you see above. I guess I should have at least expected a triangular looking torus since nine modules make make three periods, but what I got was a structure which exhibits two-fold symmetry. I had to differentially weight the inner and outer tendons to get a structure without interference problems. I did this carefully to avoid introducing additional asymmetries. With this structure, the minimum strut-tendon centerline-to-centerline clearance is 0.151 model units and the minimum strut-strut centerline-to-centerline clearance is 0.199.
The struts are colored to emphasize the double helix except there is a discontinuity at the bottom due to the fact that the design encompasses three periods which is an odd number. Because of the location of the discontinuity, the two-fold symmetry transform preserves the colors as well as the geometry.
The table below enumerates the critical statistics by member. The "Weight" value is the weight that was applied to tendons in the objective function. This is not applicable to the struts since they were all constrained to be of length 2.0 model units. It is also not applicable to the girdling tendons which mark the boundary between stages (pink in the diagram above) since they were all constrained to be of length 1.0 model units. The "Weight" value is of no interest to model builders. Only people who are interested in the mathematical programming problem that was used to design the structure will find it of interest. When the value appears as an expression, "^" indicates exponentiation, "*" indicates multiplication and "/" indicates division. The exponent is applied before any division or multiplication is done.
| Label | End Points | Length | Force | Weight | |
|---|---|---|---|---|---|
| st0103p | pt01A | pt03a | 2.00000 | -5.73504 | N/A |
| st0103q | pt01B | pt03b | 2.00000 | -3.88959 | N/A |
| side01ap | pt01A | pt03b | 1.84781 | 1.84781 | 1.00000 |
| side01bp | pt11a | pt03b | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| side01cp | pt01A | pt02B | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| side01aq | pt01B | pt03a | 1.84781 | 1.84781 | 1.00000 |
| side01bq | pt11b | pt03a | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| side01cq | pt01B | pt02A | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| gird01ap | pt02A | pt03a | 1.00000 | 0.961236 | N/A |
| gird01bp | pt02A | pt03b | 1.00000 | 2.17191 | N/A |
| gird01aq | pt02B | pt03b | 1.00000 | 0.574425 | N/A |
| gird01bq | pt02B | pt03a | 1.00000 | 3.01893 | N/A |
| st0204p | pt02A | pt04a | 2.00000 | -4.19561 | N/A |
| st0204q | pt02B | pt04b | 2.00000 | -6.01463 | N/A |
| side02ap | pt02A | pt04b | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side02bp | pt04a | pt03b | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| side02cp | pt02A | pt03A | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| side02aq | pt02B | pt04a | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side02bq | pt04b | pt03a | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| side02cq | pt02B | pt03B | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| gird02ap | pt03B | pt04a | 1.00000 | 0.110541 | N/A |
| gird02bp | pt03A | pt04a | 1.00000 | 3.88965 | N/A |
| gird02aq | pt03A | pt04b | 1.00000 | 1.04863 | N/A |
| gird02bq | pt03B | pt04b | 1.00000 | 3.88965 | N/A |
| st0305p | pt03A | pt05a | 2.00000 | -6.01463 | N/A |
| st0305q | pt03B | pt05b | 2.00000 | -4.19561 | N/A |
| side03ap | pt03A | pt05b | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side03bp | pt05a | pt04a | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| side03cp | pt03A | pt04B | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| side03aq | pt03B | pt05a | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side03bq | pt05b | pt04b | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| side03cq | pt03B | pt04A | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| gird03ap | pt04B | pt05a | 1.00000 | 3.01893 | N/A |
| gird03bp | pt04A | pt05a | 1.00000 | 0.574425 | N/A |
| gird03aq | pt04A | pt05b | 1.00000 | 2.17191 | N/A |
| gird03bq | pt04B | pt05b | 1.00000 | 0.961236 | N/A |
| st0406p | pt04A | pt06a | 2.00000 | -3.88959 | N/A |
| st0406q | pt04B | pt06b | 2.00000 | -5.73504 | N/A |
| side04ap | pt04A | pt06b | 1.84781 | 1.84781 | 1.00000 |
| side04bp | pt06a | pt05b | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| side04cp | pt04A | pt05A | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| side04aq | pt04B | pt06a | 1.84781 | 1.84781 | 1.00000 |
| side04bq | pt06b | pt05a | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| side04cq | pt04B | pt05B | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| gird04ap | pt05B | pt06a | 1.00000 | 0.574425 | N/A |
| gird04bp | pt05A | pt06a | 1.00000 | 2.17191 | N/A |
| gird04aq | pt05A | pt06b | 1.00000 | 0.961236 | N/A |
| gird04bq | pt05B | pt06b | 1.00000 | 3.01893 | N/A |
| st0507p | pt05A | pt07a | 2.00000 | -4.19561 | N/A |
| st0507q | pt05B | pt07b | 2.00000 | -6.01463 | N/A |
| side05ap | pt05A | pt07b | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side05bp | pt07a | pt06a | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| side05cp | pt05A | pt06B | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| side05aq | pt05B | pt07a | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side05bq | pt07b | pt06b | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| side05cq | pt05B | pt06A | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| gird05ap | pt06B | pt07a | 1.00000 | 3.88965 | N/A |
| gird05bp | pt06A | pt07a | 1.00000 | 0.110541 | N/A |
| gird05aq | pt06A | pt07b | 1.00000 | 3.88965 | N/A |
| gird05bq | pt06B | pt07b | 1.00000 | 1.04863 | N/A |
| st0608p | pt06A | pt08a | 2.00000 | -4.19561 | N/A |
| st0608q | pt06B | pt08b | 2.00000 | -6.01463 | N/A |
| side06ap | pt06A | pt08b | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side06bp | pt08a | pt07b | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| side06cp | pt06A | pt07A | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| side06aq | pt06B | pt08a | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side06bq | pt08b | pt07a | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| side06cq | pt06B | pt07B | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| gird06ap | pt07B | pt08a | 1.00000 | 0.961236 | N/A |
| gird06bp | pt07A | pt08a | 1.00000 | 2.17191 | N/A |
| gird06aq | pt07A | pt08b | 1.00000 | 0.574425 | N/A |
| gird06bq | pt07B | pt08b | 1.00000 | 3.01893 | N/A |
| st0709p | pt07A | pt09a | 2.00000 | -3.88959 | N/A |
| st0709q | pt07B | pt09b | 2.00000 | -5.73504 | N/A |
| side07ap | pt07A | pt09b | 1.84781 | 1.84781 | 1.00000 |
| side07bp | pt09a | pt08a | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| side07cp | pt07A | pt08B | 1.59298 | 0.972316 | 1.0/2.45^0.550929 |
| side07aq | pt07B | pt09a | 1.84781 | 1.84781 | 1.00000 |
| side07bq | pt09b | pt08b | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| side07cq | pt07B | pt08A | 1.08355 | 1.77521 | 1.0*2.45^0.550929 |
| gird07ap | pt08B | pt09a | 1.00000 | 2.17191 | N/A |
| gird07bp | pt08A | pt09a | 1.00000 | 0.574425 | N/A |
| gird07aq | pt08A | pt09b | 1.00000 | 3.01893 | N/A |
| gird07bq | pt08B | pt09b | 1.00000 | 0.961236 | N/A |
| st0810p | pt08A | pt10a | 2.00000 | -6.01463 | N/A |
| st0810q | pt08B | pt10b | 2.00000 | -4.19561 | N/A |
| side08ap | pt08A | pt10b | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side08bp | pt10a | pt09b | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| side08cp | pt08A | pt09A | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| side08aq | pt08B | pt10a | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side08bq | pt10b | pt09a | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| side08cq | pt08B | pt09B | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| gird08ap | pt09B | pt10a | 1.00000 | 1.04863 | N/A |
| gird08bp | pt09A | pt10a | 1.00000 | 3.88965 | N/A |
| gird08aq | pt09A | pt10b | 1.00000 | 0.110541 | N/A |
| gird08bq | pt09B | pt10b | 1.00000 | 3.88965 | N/A |
| st0911p | pt09A | pt11a | 2.00000 | -4.19561 | N/A |
| st0911q | pt09B | pt11b | 2.00000 | -6.01463 | N/A |
| side09ap | pt09A | pt11b | 1.35013 | 2.71586 | 1.0*2.45^0.779954 |
| side09bp | pt11a | pt10a | 1.86981 | 0.788819 | 1.0/2.45^0.963138 |
| side09cp | pt09A | pt01B | 1.11558 | 1.23002 | 1.0*2.45^0.108978 |
| side09aq | pt09B | pt11a | 1.81772 | 0.903641 | 1.0/2.45^0.779954 |
| side09bq | pt11b | pt10b | 1.04442 | 2.47569 | 1.0*2.45^0.963138 |
| side09cq | pt09B | pt01A | 1.16002 | 1.05210 | 1.0/2.45^0.108978 |
| gird09ap | pt01B | pt11a | 1.00000 | 2.17191 | N/A |
| gird09bp | pt01A | pt11a | 1.00000 | 0.961236 | N/A |
| gird09aq | pt01A | pt11b | 1.00000 | 3.01893 | N/A |
| gird09bq | pt01B | pt11b | 1.00000 | 0.574425 | N/A |
The design for this structure was completed September 21, 2004.