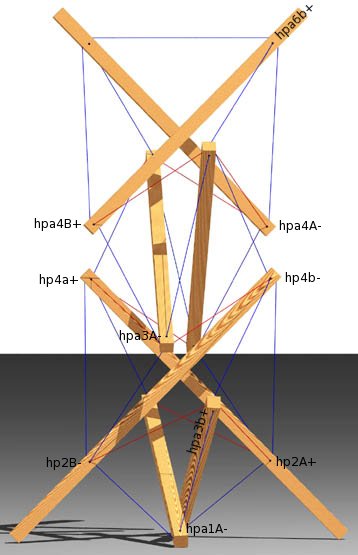
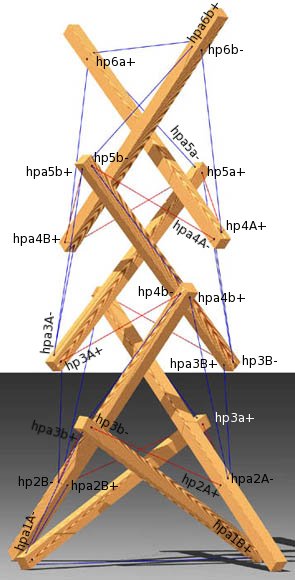
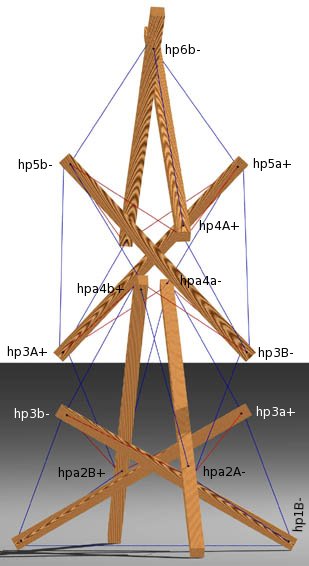
Hub Constructs
These items are just vectors corresponding to each of the
struts (see Member Descriptions below). Some are normalized.
The normalized -- to 1 inch (stvn..) and 0.25 inch (stvq..) --
versions are used as offsets for constructing hub points. Some
(hva..) are cross products, constructed to be orthogonal to the
primary vectors (hv..).
<DiffVec> stv13 p1A p3a
<ScaledVec> stvn13 stv13 1/29
<ScaledVec> stvq13 stv13 1/(29*4)
<DiffVec> stv24 p4a p2A
<ScaledVec> stvn24 stv24 1/29
<ScaledVec> stvq24 stv24 1/(29*4)
<DiffVec> stv35 p3A p5a
<ScaledVec> stvn35 stv35 1/29
<ScaledVec> stvq35 stv35 1/(29*4)
<DiffVec> stv46 p4A p6a
<ScaledVec> stvn46 stv46 1/29
<ScaledVec> stvq46 stv46 1/(29*4)
<CrossVec> hva13 hv13 stvn13
<CrossVec> hva24 hv24 stvn24
<CrossVec> hva35 hv35 stvn35
<CrossVec> hva46 hv46 stvn46
Hub Constraints
These are constraints the primary vectors must meet.
Since the tensegrity is constructed of 1-7/16 inch square
stock, the vectors are constrained to be 0.71875 inches
long and orthogonal to their respective struts.
<VecDotVec> hvdot13 stv13 hv13 1.0 0.0 Con
<VecLength> hvlen13 hv13 1.0 sqr(0.71875) Con
<VecDotVec> hvdot24 stv24 hv24 1.0 0.0 Con
<VecLength> hvlen24 hv24 1.0 sqr(0.71875) Con
<VecDotVec> hvdot35 stv35 hv35 1.0 0.0 Con
<VecLength> hvlen35 hv35 1.0 sqr(0.71875) Con
<VecDotVec> hvdot46 stv46 hv46 1.0 0.0 Con
<VecLength> hvlen46 hv46 1.0 sqr(0.71875) Con
Hub Connectivity
This shows how the primary vectors and Hub Constructs are
applied to the primary points (p..) to derive tendon attachment
points (hp... and hpa...).
# intermediate hub points
<VecPt> pq1A p1A + stvq13
<VecPt> pq3a p3a + stvq13
<VecPt> pq2A p2A - stvq24
<VecPt> pq4a p4a - stvq24
<VecPt> pq3A p3A + stvq35
<VecPt> pq5a p5a + stvq35
<VecPt> pq4A p4A + stvq46
<VecPt> pq6a p6a + stvq46
# tendon attachment points
<VecPt> hp1A+ pq1A + hv13
<VecPt> hp1A- pq1A - hv13
<VecPt> hp3a+ pq3a + hv13
<VecPt> hp3a- pq3a - hv13
<VecPt> hp2A+ pq2A + hv24
<VecPt> hp2A- pq2A - hv24
<VecPt> hp4a+ pq4a + hv24
<VecPt> hp4a- pq4a - hv24
<VecPt> hp3A+ pq3A + hv35
<VecPt> hp3A- pq3A - hv35
<VecPt> hp5a+ pq5a + hv35
<VecPt> hp5a- pq5a - hv35
<VecPt> hp4A+ p4A + hv46
<VecPt> hp4A- p4A - hv46
<VecPt> hp6a+ p6a + hv46
<VecPt> hp6a- p6a - hv46
# tendon attachment points
<VecPt> hpa1A+ p1A + hva13
<VecPt> hpa1A- p1A - hva13
<VecPt> hpa3a+ p3a + hva13
<VecPt> hpa3a- p3a - hva13
<VecPt> hpa2A+ p2A + hva24
<VecPt> hpa2A- p2A - hva24
<VecPt> hpa4a+ p4a + hva24
<VecPt> hpa4a- p4a - hva24
<VecPt> hpa3A+ p3A + hva35
<VecPt> hpa3A- p3A - hva35
<VecPt> hpa5a+ p5a + hva35
<VecPt> hpa5a- p5a - hva35
<VecPt> hpa4A+ pq4A + hva46
<VecPt> hpa4A- pq4A - hva46
<VecPt> hpa6a+ pq6a + hva46
<VecPt> hpa6a- pq6a - hva46
Transformations
This shows how transforms are defined and how they are
applied to derive transformed objects from basic objects.
In this case, there is just one transform which amounts
to a 180° rotation about the z-axis.
# permutations
<Per> p-x-y+z -X -Y Z
# transform points
<XformPt> p1B p1A p-x-y+z
<XformPt> p2B p2A p-x-y+z
<XformPt> p3B p3A p-x-y+z
<XformPt> p3b p3a p-x-y+z
<XformPt> p4B p4A p-x-y+z
<XformPt> p4b p4a p-x-y+z
<XformPt> p5b p5a p-x-y+z
<XformPt> p6b p6a p-x-y+z
...
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# members -- first stage
<Member> end1 hpa1A+ hpa1B+ 0.0 sqr(28.9681785040537) 4 Con *
<Member> st13 p1A p3a 0.0 sqr(29) 1 Con CalcClear *
<Member> side1a hpa1A- hpa3b+ 0.96 0.0 3 Obj *
<Member> side1c hp1A- hpa2B+ 0.96 0.0 3 Obj *
<Member> gird1a hp2A- hp3a+ 0.0 sqr(29/1.88) 2 Con *
<Member> gird1b hp2A+ hp3b- 0.0 sqr(29/1.88) 2 Con *
# members -- second (complete) stage
<Member> st24 p4a p2A 0.0 sqr(29) 1 Con CalcClear *
<Member> side2a hpa2A- hpa4b+ 1.0 0.0 3 Obj *
<Member> side2b hp4a- hpa3a- 1.0 0.0 3 Obj *
<Member> side2c hp2A- hpa3B+ 1.0 0.0 3 Obj *
<Member> gird2a hp4a- hp3B+ 0.0 sqr(29/1.88) 2 Con *
<Member> gird2b hp4a+ hp3A- 0.0 sqr(29/1.88) 2 Con *
# members -- third (complete) stage
<Member> st35 p3A p5a 0.0 sqr(29) 1 Con CalcClear *
<Member> side3a hpa3A- hpa5b+ 1.15 0.0 3 Obj *
<Member> side3b hp5a- hpa4a- 1.0 0.0 3 Obj *
<Member> side3c hp3A- hp4B- 1.0 0.0 3 Obj *
<Member> gird3a hp5a- hpa4B- 0.0 sqr(29/1.88) 2 Con *
<Member> gird3b hp5a+ hpa4A+ 0.0 sqr(29/1.88) 2 Con *
# members -- fourth and last stage
<Member> st46 p4A p6a 0.0 sqr(29) 1 Con CalcClear *
<Member> side4a hp4A+ hp6b- 1.23 0.0 3 Obj *
<Member> side4b hpa6a+ hpa5a- 1.23 0.0 3 Obj *
<Member> end2 hp6b+ hp6a+ 0.0 sqr(1.3*(29/1.88)) 4 Con *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
tendon attachment point to tendon attachment point on one
side of the strut. The values are in model units which in
this case is inches.
end1: 28.9682 st13: 29 side1a: 14.4777
side1c: 16.3706 gird1a: 15.4255 gird1b: 15.4255
st24: 29 side2a: 20.3892 side2b: 16.8387
side2c: 16.4146 gird2a: 15.4255 gird2b: 15.4255
st35: 29 side3a: 20.7575 side3b: 16.4394
side3c: 16.3934 gird3a: 15.4255 gird3b: 15.4255
st46: 29 side4a: 19.9515 side4b: 16.4151
end2: 20.0532
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
Since the symmetry transform maps end1 and end2 into
themselves, they each represent two overlapping tendons,
each with the force magnitude given below. So, the total
force is actually twice the value given for end1 and end2.
Force Magnitudes
end1: 9.49886 st13: -38.9349 side1a: 13.8986
side1c: 15.7158 gird1a: 22.4882 gird1b: 28.6662
st24: -64.4141 side2a: 20.3892 side2b: 16.8387
side2c: 16.4146 gird2a: 28.0198 gird2b: 27.416
st35: -67.1562 side3a: 23.8711 side3b: 16.4394
side3c: 16.3934 gird3a: 25.4476 gird3b: 29.6394
st46: -54.5831 side4a: 24.5403 side4b: 20.1906
end2: 14.2609
Average tendon force magnitude: 20.5627
Tendon Construction Lengths (in inches, 16ths and 32nds)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for a member
represents the distance between the locations where it
departs from the hub. The struts were cut from 1.5-inch by
1.5-inch cedar balusters. The lengths below are specified
for doubled strands of braided nylon twine (e.g. T.W. Evans
#1 Braided Nylon Mason Line -- Item No. 12-503). Its behavior
under stress is highly non-linear, so a look-up table
was used to compute strains. It seems to be
slightly more stretchy than twine composed of twisted strands
(e.g. Wellington #18 Nylon Twine -- Prod. No. 46302).
Prestress forces were assumed to affect tendon lengths and
not strut lengths.
Average Tendon Force Magnitude (chart units)> 30 pounds
Length Scale Factor> 1.0
(Things are scaled so model and construction units are the same.)
Strut and Tendon Hub Adjustments> 0.0 0.0
(Hub connections were handled explicity in the nonlinear
programming problem, so no ad hoc adjustment is needed here
to account for the tendon hub connections. All the strut
lengths were handled in ad hoc ways described below.)
end1: 26 8 0 st13: 29 0 0 side1a: 13 8 0 side1c: 15 2 1
gird1a: 13 15 0 gird1b: 13 12 0 st24: 29 0 0 side2a: 18 9 0
side2b: 15 8 0 side2c: 15 2 1 gird2a: 13 12 1 gird2b: 13 12 1
st35: 29 0 0 side3a: 18 11 0 side3b: 15 2 1 side3c: 15 2 0
gird3a: 13 13 1 gird3b: 13 11 1 st46: 29 0 0 side4a: 17 15 0
side4b: 14 15 0 end2: 17 14 0
Strut Construction
The struts have 0.25-inch diameter holes drilled in
them for tendon attachment. Each hub has two holes
drilled at right angles offset 0.25 inch from each
other so that their interiors are tangent to each
other but don't overlap. The first hole is
drilled so its center is 0.75 inch from one end of
the strut. The second hole is drilled at a right
angle so its center is 1 inch from the same end.
The third hole is drilled parallel to the second so
its center is 29 inches from the center of the
second hole. Back up a quarter of an inch and drill
the fourth hole perpendicular to the third. It is
parallel to the first hole and its center is 29 inches
from the center of the first hole. The lengths of
st13, st24, st35 and st46 are 30.75, 42, 30.75 and
34.75 inches respectively.
Material Quantities
This provides an estimate of how much twine will
be needed to assemble the structure. The strut material
necessary must be estimated manually, and amounts to
276.5 inches.
Length Scale Factor> 1.0
Tendon Adjustment> (-7.5)
(adjust the tendon lengths by adding 7.5 inches to both
ends)
Cross
Type Section Quantity Count
4 1 142.908 4
3 2 594.463 20
2 2 326.609 12
Tndns 1985.05 36
 |
 |
 |
| Three Views of the Trellis/Plant Hanger | ||
structure file: chain/x2l4chain1b.rc variable file: chain/x2l4chain1b.dat stress-strain chart file: v02oct_s/evans.ssc cross-section table: chain/x2l4chain1b.cst digit list file: src/standard.dls |
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com