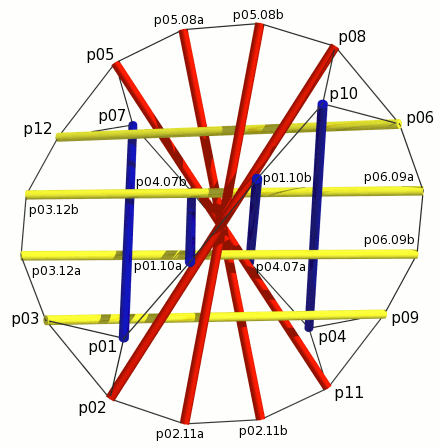
3v Pars T-Tetra with Point Labels
structure file: v2tetra/pars/pzzttnox1.rc
variable file: v2tetra/pars/pzzttnox1.dat
digit list: src/mm.dls
|
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# struts
<Member> s01.07 p01 p07 0.00 sqr(4.0925) 1 Con *
<Member> s02.08 p02 p08 0.00 sqr(4.0925) 1 Con *
<Member> s03.09 p03 p09 0.00 sqr(4.0925) 1 Con *
<Member> s04.10 p04 p10 0.00 sqr(4.0925) 1 Con *
<Member> s05.11 p05 p11 0.00 sqr(4.0925) 1 Con *
<Member> s06.12 p06 p12 0.00 sqr(4.0925) 1 Con *
<Member> s01.10.04.07a p01.10a p04.07b 0.00 sqr(4.0925) 9 Con *
<Member> s01.10.04.07b p01.10b p04.07a 0.00 sqr(4.0925) 9 Con *
<Member> s02.11.05.08a p02.11a p05.08b 0.00 sqr(4.0925) 9 Con *
<Member> s02.11.05.08b p02.11b p05.08a 0.00 sqr(4.0925) 9 Con *
<Member> s03.12.06.09a p03.12a p06.09b 0.00 sqr(4.0925) 9 Con *
<Member> s03.12.06.09b p03.12b p06.09a 0.00 sqr(4.0925) 9 Con *
# triangle tendons
<Member> t01.03 p01 p03 0.00 1.00 2 Con *
<Member> t02.01 p02 p01 0.00 1.00 2 Con *
<Member> t03.02 p03 p02 0.00 1.00 2 Con *
<Member> t04.09 p04 p09 0.00 1.00 2 Con *
<Member> t05.07 p05 p07 0.00 1.00 2 Con *
<Member> t06.08 p06 p08 0.00 1.00 2 Con *
<Member> t07.12 p07 p12 0.00 1.00 2 Con *
<Member> t08.10 p08 p10 0.00 1.00 2 Con *
<Member> t09.11 p09 p11 0.00 1.00 2 Con *
<Member> t10.06 p10 p06 0.00 1.00 2 Con *
<Member> t11.04 p11 p04 0.00 1.00 2 Con *
<Member> t12.05 p12 p05 0.00 1.00 2 Con *
# zig-zag tendons
<Member> z01.10a p01 p01.10a 1.00 1.00 3 Con *
<Member> z01.10b p01.10a p01.10b 1.00 0.00 3 Obj *
<Member> z01.10c p01.10b p10 1.00 1.00 3 Con *
<Member> z02.11a p02 p02.11a 1.00 1.00 3 Con *
<Member> z02.11b p02.11a p02.11b 1.00 0.00 3 Obj *
<Member> z02.11c p02.11b p11 1.00 1.00 3 Con *
<Member> z03.12a p03 p03.12a 1.00 1.00 3 Con *
<Member> z03.12b p03.12a p03.12b 1.00 0.00 3 Obj *
<Member> z03.12c p03.12b p12 1.00 1.00 3 Con *
<Member> z04.07a p04 p04.07a 1.00 1.00 3 Con *
<Member> z04.07b p04.07a p04.07b 1.00 0.00 3 Obj *
<Member> z04.07c p04.07b p07 1.00 1.00 3 Con *
<Member> z05.08a p05 p05.08a 1.00 1.00 3 Con *
<Member> z05.08b p05.08a p05.08b 1.00 0.00 3 Obj *
<Member> z05.08c p05.08b p08 1.00 1.00 3 Con *
<Member> z06.09a p06 p06.09a 1.00 1.00 3 Con *
<Member> z06.09b p06.09a p06.09b 1.00 0.00 3 Obj *
<Member> z06.09c p06.09b p09 1.00 1.00 3 Con *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from pin insertion
point to pin insertion point, as are the tendon lengths.
The values are in model units.
s01.07: 4.0925 s02.08: 4.0925 s03.09: 4.0925
s04.10: 4.0925 s05.11: 4.0925 s06.12: 4.0925
s01.10.04.07a: 4.0925 s01.10.04.07b: 4.0925 s02.11.05.08a: 4.0925
s02.11.05.08b: 4.0925 s03.12.06.09a: 4.0925 s03.12.06.09b: 4.0925
t01.03: 1 t02.01: 1 t03.02: 1
t04.09: 1 t05.07: 1 t06.08: 1
t07.12: 1 t08.10: 1 t09.11: 1
t10.06: 1 t11.04: 1 t12.05: 1
z01.10a: 1 z01.10b: 1.00001 z01.10c: 1
z02.11a: 1 z02.11b: 1.00001 z02.11c: 1
z03.12a: 1 z03.12b: 1.00001 z03.12c: 1
z04.07a: 1 z04.07b: 1.00001 z04.07c: 1
z05.08a: 1 z05.08b: 1.00001 z05.08c: 1
z06.09a: 1 z06.09b: 1.00001 z06.09c: 1
Relative Member Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
s01.07: -0.768474 s02.08: -0.768474 s03.09: -0.768474
s04.10: -0.768474 s05.11: -0.768474 s06.12: -0.768474
s01.10.04.07a: -0.294165 s01.10.04.07b: -0.294165 s02.11.05.08a: -0.294165
s02.11.05.08b: -0.294165 s03.12.06.09a: -0.294165 s03.12.06.09b: -0.294165
t01.03: 0.674415 t02.01: 0.674415 t03.02: 0.674415
t04.09: 0.674415 t05.07: 0.674415 t06.08: 0.674415
t07.12: 0.674415 t08.10: 0.674415 t09.11: 0.674415
t10.06: 0.674415 t11.04: 0.674415 t12.05: 0.674415
z01.10a: 1.00001 z01.10b: 1.00001 z01.10c: 1.00001
z02.11a: 1.00001 z02.11b: 1.00001 z02.11c: 1.00001
z03.12a: 1.00001 z03.12b: 1.00001 z03.12c: 1.00001
z04.07a: 1.00001 z04.07b: 1.00001 z04.07c: 1.00001
z05.08a: 1.00001 z05.08b: 1.00001 z05.08c: 1.00001
z06.09a: 1.00001 z06.09b: 1.00001 z06.09c: 1.00001
Average tendon force magnitude: 0.869769
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of the 3/16-inch-diameter wooden dowel.
The tendons were made of 12-lb.-test braided nylon fishing line.
In this case, the attachment point at the hubs was a simple
metal pin stuck into the end of the strut, so no member-length
adjustments were necessary. Prestress forces are assumed
not to affect strut lengths.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 200/4.0925
Strut and Tendon Hub Adjustments - s;t> 0 0
At the level of accuracy here, it turns out all the struts have
the same length, as do all the tendons.
strut 200 0
tendon 48 0
Material Quantities (in millimeters)
Estimates of the total amount of material required to build
the structure. The adjustment in this case includes "waste":
for the strut, the amount lost when sawing the strut from a
length of dowel (1 mm from each end); for the tendons, the amount
of extra needed to successfully tie the tendon (50 mm extra at
each end).
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 200/4.0925
Strut and Tendon Adjustments - s;t> -1, -50
Cross
Type Section Quantity Count
1 1 1212 6
9 1 1212 6
2 1 1759.16 12
3 1 2619.43 18
Strts 2424 12
Tndns 4378.58 30

3v Pars T-Tetra with Point Labels
structure file: v2tetra/pars/pzzttnox1.rc
variable file: v2tetra/pars/pzzttnox1.dat
digit list: src/mm.dls
|
|
CONTACT: Bob Burkhardt Tensegrity Solutions Box 426164 Cambridge, MA 02142-0021 USA e-mail: bobwb@juno.com |