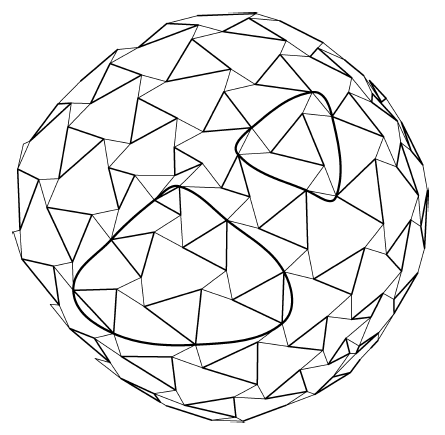
Figure 6.1: Valid Tensegrity Truncation Groups
A Practical Guide to Tensegrity Design
Table of Contents
5 Double-Layer Tensegrities
Chapter 6
Double-Layer Tensegrity Domes
6.1 Double-Layer Tensegrity Domes: Introduction
Tensegrity spheres seem appropriate for environments where external loads are evenly distributed about the surfaces of structures. Examples of this type of environment are underground, underwater, the atmosphere and outer space. For planetary surfaces, truncated structures, domes, are more likely to find favor since the base of such structures provides an effective way of dissipating the concentrated load of gravity as well as a needed source of floor space within the structure. A dome might also make an interesting sort of bay window when attached to the flat side of a more conventional structure. With these considerations in mind, a method of truncating double-layer spherical tensegrity structures is presented in this chapter.
Truncating a single-layer tensegrity sphere amounts to removing a vertex-tangent group of triangles or other low-frequency polylaterals and replacing them with a single polylateral of high frequency. This high-frequency polylateral, the base mentioned above, is tangent with the remaining polylaterals at the vertexes which were touched by the removed polylaterals.
 Figure 6.1: Valid Tensegrity Truncation Groups |
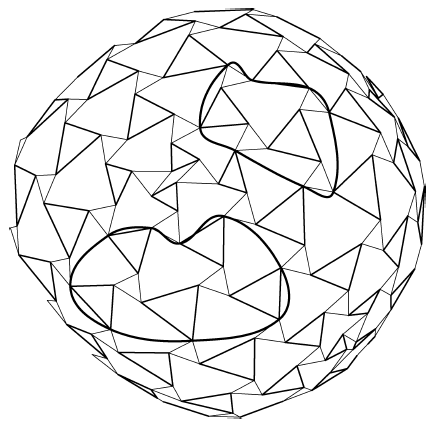 Figure 6.2: Invalid Tensegrity Truncation Groups |
To have a workable tensegrity, the truncation must be done so that each vertex of the new polylateral is tangent with exactly one vertex of one of the remaining original polylaterals. Situations where the new polylateral is tangent at more than one point with one of the original polylaterals are not admissible. This represents a restriction on the groups of polylaterals which can be removed. Figures 6.1 and 6.2 illustrate groups which meet and do not meet this restriction. Even with this restriction, single-layer truncated tensegrities don't seem practical since the re-routing of the struts in the neighborhood of the truncation invariably results in intractable interference problems.
For double-layer tensegrities where the tendon network is conceived of as an alternating set of polylaterals as is described in Section 5.2, an additional restriction is necessary: the remaining polylaterals tangent to the new polylateral must all belong to the same alternation group. This ensures the new polylateral is a well-defined member of the alternation group alternate to that of the remaining polylaterals tangent to it. In addition, the problem with re-routing struts which plagues single-layer structures is avoided in double-layer structures if the truncation polylateral is chosen so that it approximates a great circle; that is, the polylateral has no sharp turns.
A significant problem posed by a truncation is a loss of symmetry. This has the undesirable effect of greatly increasing the size of the programming problem whose solution is required to generate a structure at a given frequency. There is not much way around this unfortunately.
The large truncation needed to provide a base for a dome can also cause a structure to deviate to a great extent from its original configuration. These deviations are usually in a way which cause the base area to contract relative to the original cross-section it had in the sphere. These deviations can also introduce new, intractable interference problems. So, for this type of truncation, it is often desirable to fix all the points of the new polylateral and perhaps further adjust them to lie in a plane and observe other convenient regularities. Such constraints can also be desirable from the point of view of easing the processes of designing and building a foundation for the dome.
Attaching the dome to its base means introducing the material on which the dome is situated as a structural member which constrains the base points to stay at specified fixed positions. Such a structure is no longer a tensegrity according to some definitions since it now depends on the base material to help shape it. It is no longer self-supporting.
Introducing guys to stiffen the connection between the structure and the surface it is attached to is also advisable.
Table of Contents
6.2 A Procedure for Designing Double-Layer
Tensegrity Domes