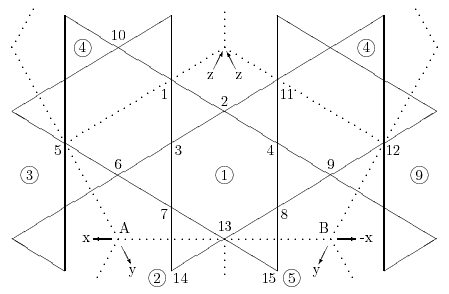
Figure 6.3: 6ν T-Octahedron Sphere: Symmetry Regions
A Practical Guide to Tensegrity Design
Table of Contents
6.1 Double-Layer Tensegrity Domes:
Introduction
6.2 Double-Layer Tensegrity Domes: An Example
The following steps implement the design of a double-layer dome like that described in Section 6.1:
| Step 1 | Solve the tensegrity programming problem for the sphere. |
| Step 2 | Implement the topological changes required by the truncation. |
| Step 3 | Adjust the base points (the points of the truncation polylateral as they manifest themselves on the inner tendon network) so they lie evenly-spaced on a circle which approximates as closely as possible their unadjusted positions in the original sphere. |
| Step 4 | Add guys. |
| Step 5 | Using the coordinate values from the sphere as initial values, solve the tensegrity programming problem for the dome. |
| Step 6 | Make necessary adjustments to fix member force and interference problems. |
To illustrate this method for truncating double-layer spheres, the tensegrity based on the 6ν octahedron is useful. It has a low-enough frequency to be pedagogically tractable and a high-enough frequency that the appearance of higher-frequency structures can be anticipated in studying it.
6.2.1 Dome Step 1: Compute the sphere
Figures 6.3 and 6.4 diagram the basic triangle network for the 6ν double-layer tensegrity octahedron sphere and a coordinate system for its analysis in the same manner as Figures 5.3 and 5.5 did for the 4ν version of the sphere in Section 5.3. The main difference is that, with the higher frequency, there is more of everything. For example, now the struts in Figure 6.4 are clustered about three basic t-tripods instead of two as in Figure 5.5.
Table 6.1 enumerates the members of this 6ν version of the double-layer sphere. The anomalous value of 1.5 for the length of Member #33 in Table 6.1 is chosen in light of experience with the 4ν structure.1
The weights for the inner and outer binding tendons in the objective function are derived using the formula where the values used for are 1.2 and 0.5 respectively for the inner and outer binding tendons. and represent the spherical excess corresponding to the initial values of the two end points of the tendon.2 The spherical excess is the amount the sphere radius exceeds the distance of the unprojected point from the center of the octahedron. This number is calculated as a ratio and is always greater than or equal to 1.0. It is equal to 1.0 at the vertexes of the octahedron. Giving a smaller weight to the tendons distant from the vertexes of the basis octahedron allows them to be longer than they would otherwise be. This allows the octahedral faces to bulge out more than they would otherwise and gives the structure a more spherical, less faceted, look. The objective-function weights for the primary and secondary interlayer tendons are 2.0 and 1.4 respectively independent of any spherical excess values.
 Figure 6.3: 6ν T-Octahedron Sphere: Symmetry Regions |
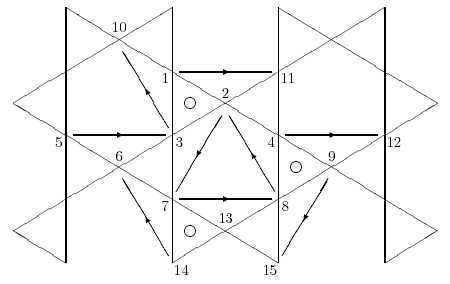 Figure 6.4: 6ν T-Octahedron Sphere: Truss Members |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.1: 6ν T-Octahedron Sphere: Truss Members |
As with the 4ν version of this sphere, the derivation of the initial point values is facilitated by the use of the geodesic breakdown. Kenner's tables3 are used to generate initial point coordinates. Again, Kenner's table has to be expanded by rotating all the points about the axis by 90°. Table 6.2 outlines the correspondence between the basic points and his coordinate system. (Rotated points are indicated with an asterisk.)
| ||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.2: 6ν T-Octahedron: Angular Point Coordinates |
The initial coordinate values for inner and outer realizations of these points are summarized in Table 6.3. These are derived from the angular values in Table 6.2 with inner and outer radiuses applied. The inner radius (3.15) is chosen so the triangle tendon lengths average approximately 1 (0.995729). The outer radius (5.15) is chosen so strut lengths in the double-layer versions of the structure would initially average approximately 3 (2.94314). The implied initial lengths are summarized in Table 6.4.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.3: 6ν T-Octahedron Sphere: Initial Basic Point Coordinates |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.4: 6ν T-Octahedron Sphere: Initial Member Lengths |
The derivation of the symmetry points from the basic points is shown in Table 6.5. The symmetry transforms on which this table is based are enumerated in Table 5.5. Outer points follow the same symmetries as inner points.
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.5: 6ν T-Octahedron Sphere: Symmetry Point Correspondences |
The structure is computed by minimizing a weighted combination of the interlayer and binding tendons subject to constraints on the struts and convergence tendons. Two initial iterations are done using the penalty formulation in conjunction with Fletcher-Reeves to bring the initial points into approximate conformance with the constraints. After this five iterations are done with the exact formulation in conjunction with Fletcher-Reeves to bring the values to convergence. The derivatives of the objective function with respect to the independent coordinate values are all less than .
Tables 6.6 and 6.7 show the values for the final lengths and relative forces.4 Table 6.8 shows the final values for the coordinates of the basic points. Figure 6.5 shows how the final version of the spherical structure appears as viewed from outside one of the octahedral vertices. For clarity, interlayer tendons have been excluded and members in the background have been eliminated by truncation. For reference, selected points in Figure 6.5 are labeled.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.6: 6ν T-Octahedron Sphere: Final Member Lengths |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.7: 6ν T-Octahedron Sphere: Final Member Forces |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.8: 6ν T-Octahedron: Final Basic Point Coordinates |
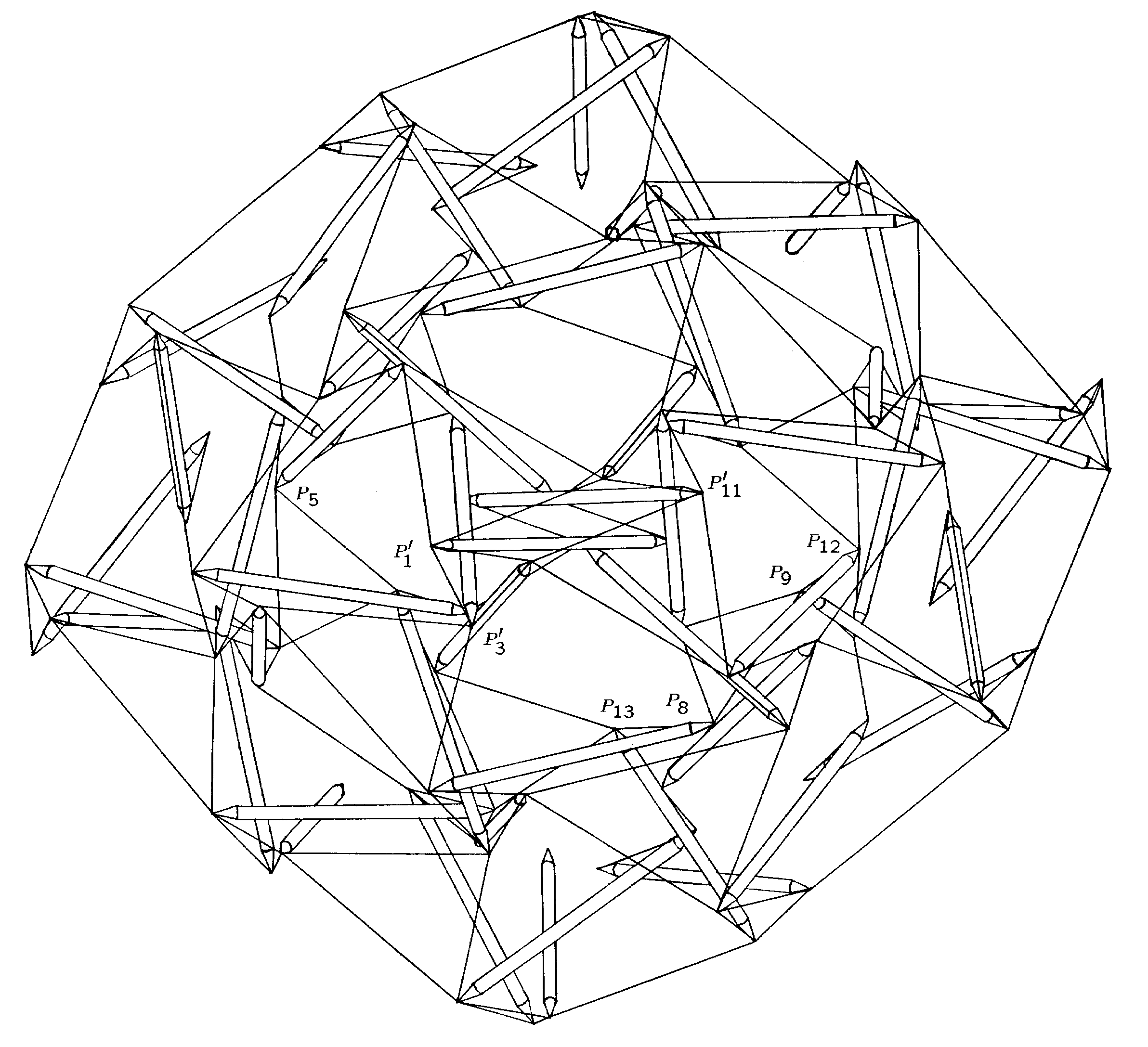 Figure 6.5: 6ν T-Octahedron Sphere: Vertex View |
1 See Section 8.2.3 for details on this exception as it is introduced to the 4ν structure.
2 stands for bulge.
3 Kenner76, "Octahedron Class I Coordinates: Frequencies 12, 6, 3", column 6ν, p. 126.
4 See Section 7.2 for the method of computing relative forces.
Table of Contents
6.2.2 Dome Step 2: Implement the truncation