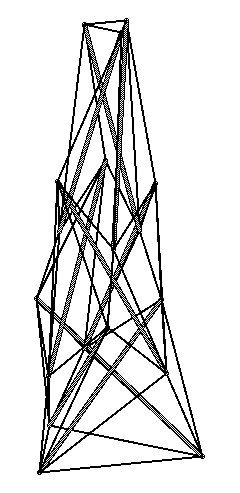
 |
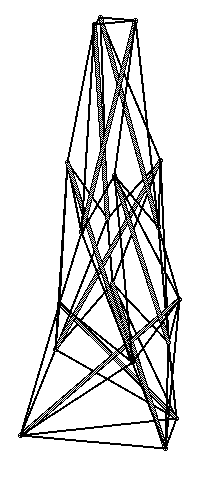 |
(VRML Model)
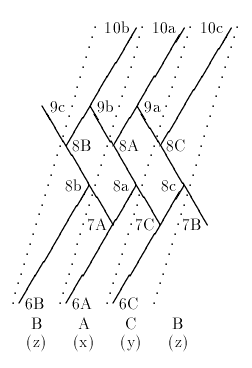
Schematic for the Tensegrity Bean Teepee
structure file: obelisk2/stage4.rc
variable file: obelisk2/stage4.dat
stress-strain chart file: v04oct_d/wellingtn.ssc
digit list file: src/standard.dls
|
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
<Member> strut0608 pt06A pt08a 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> strut0709 pt07A pt09c 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> strut0810 pt08A pt10a 0.0 sqr(2.5) 1 Con CalcClear Inelastic *
<Member> baset pt06A pt06B 0.0 sqr(2.0) 10 Con *
<Member> apext pt10a pt10b 0.0 sqr(0.5) 10 Con *
<Member> guy0 pt06A pt07B 0.55 0.0 3 Obj *
<Member> guy6 pt06A pt08b 0.35 0.0 3 Obj *
<Member> guy7 pt07A pt09b 0.40 0.0 3 Obj *
<Member> guy8 pt08A pt10b 0.70 0.0 3 Obj *
<Member> xtr8 pt08a pt08A 0.36 0.0 7 Obj *
<Member> TL0607 pt06A pt07A 0.25 0.0 4 Obj *
<Member> TS0708 pt07A pt08a 1.45 0.0 2 Obj *
<Member> TL0708 pt07A pt08B 0.55 0.0 4 Obj *
<Member> tS0708 pt07A pt08b 1.45 0.0 2 Obj *
<Member> TS0809 pt08A pt09b 1.45 0.0 2 Obj *
<Member> tS0809 pt08A pt09a 1.45 0.0 2 Obj *
<Member> tL0809 pt08c pt09a 0.55 0.0 4 Obj *
<Member> tL0910 pt09a pt10a 0.55 0.0 4 Obj *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
hub center to hub center, as are the tendon lengths.
These values are in model units.
strut0608: 2.5 strut0709: 2.5 strut0810: 2.5
baset: 2 apext: 0.5 guy0: 1.06079
guy6: 1.76225 guy7: 2.16525 guy8: 2.39895
xtr8: 0.855865 TL0607: 1.82586 TS0708: 0.940875
TL0708: 1.61585 tS0708: 1.09291 TS0809: 0.957033
tS0809: 0.851856 tL0809: 1.68392 tL0910: 1.80869
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
strut0608: -2.06741 strut0709: -3.22737 strut0810: -2.72331
baset: 0.467791 apext: 0.424326 guy0: 0.583432
guy6: 0.616788 guy7: 0.866101 guy8: 1.67927
xtr8: 0.308111 TL0607: 0.456466 TS0708: 1.36427
TL0708: 0.888719 tS0708: 1.58471 TS0809: 1.3877
tS0809: 1.23519 tL0809: 0.926157 tL0910: 0.994779
Average tendon force magnitude: 0.918921
Construction Lengths (in inches, 16ths and 32nds)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for a member
represents the distance between the locations where it
departs from the hub. The struts were cut from
1-inch by 1-inch hardwood garden stakes. The tendon material
was single strands of twisted #18 nylon twine. Its behavior
under stress is highly non-linear, so a look-up table
was used to compute strains. Prestress forces were assumed
to affect tendon lengths and not strut lengths.
Average Tendon Force Magnitude (chart units)> 20
Length Scale Factor> 42/2.5
Strut and Tendon Hub Adjustments> 0 0.5
(adjust the tendon lengths by subtracting a half inch from
both ends)
strut0608: 42 0 0 strut0709: 42 0 0 strut0810: 42 0 0 baset: 30 13 1
apext: 7 0 1 guy0: 15 12 0 guy6: 26 11 0 guy7: 32 7 1
guy8: 34 9 1 xtr8: 12 13 1 TL0607: 28 1 1 TS0708: 13 3 1
TL0708: 23 15 1 tS0708: 15 5 1 TS0809: 13 7 0 tS0809: 11 15 1
tL0809: 24 15 1 tL0910: 26 12 0
Base chord length = (2/2.5)*42" = 33.6" = 33 9 1
Material Quantities
This provides an estimate of how much material will
be needed to assemble the structure, in this case
inches of garden stake and inches of nylon twine.
The lengths must be adjusted to take into account the
fact that the strut extends past the hub and some length
of tendon is required to tie it to the strut.
The Quantity value given for each Type does not take
into account the Cross Section value. The total
Quantity given across from Tndns does.
Length Scale Factor> 42/2.5
Strut and Tendon Adjustments> 0 (-6)
Cross
Type Section Quantity Count
1 1 378 9
10 1 187.536 6
3 1 509.07 12
7 1 76.03 3
4 1 417.702 12
2 1 301.048 12
Strts 378 9
Tndns 1491.39 45
 |
 |

Schematic for the Tensegrity Bean Teepee
structure file: obelisk2/stage4.rc
variable file: obelisk2/stage4.dat
stress-strain chart file: v04oct_d/wellingtn.ssc
digit list file: src/standard.dls
|
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com