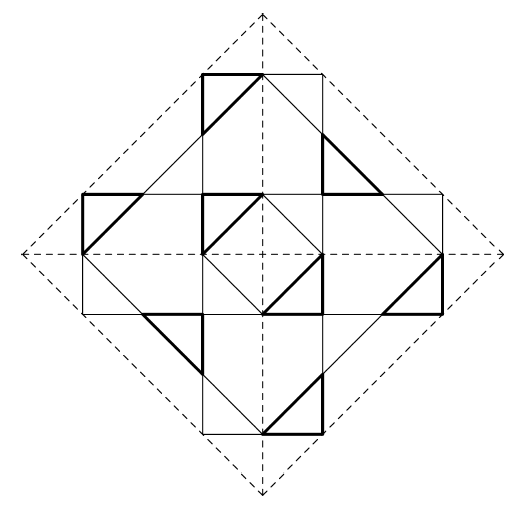
Figure 5.2: 4ν Octahedron: Alternating Triangles (Vertex View)
A Practical Guide to Tensegrity Design
Table of Contents
5.2 Double-Layer Tensegrities: Trusses
5.3 Double-Layer Tensegrities: Geodesic Networks
A network topology suitable for tensegrity designs can be obtained from an even-frequency Class I subdivision of the triangular faces of the tetrahedron, octahedron or icosahedron. Alternatively, Class II subdivisions of these same polyhedra can be used if the frequency is a multiple of four.6 Network topologies generated this way are referred to as geodesic networks since they are based on subdivision systems used to design geodesic domes. A Class I subdivision is illustrated in Figure 4.2. Only Class I subdivisions are used in this book.
 Figure 5.2: 4ν Octahedron: Alternating Triangles (Vertex View) |
A 4ν breakdown of the octahedron serves for the example of this method of generating tensegrity trusses. The portion of this breakdown relevant to tensegrity structures is shown in Figure 5.2. The breakdown triangles are shown with solid lines, and the edges of the base octahedron are shown as dashed lines.
The first step in constructing the tensegrity is to divide the resulting network into two sets of alternating triangles. In Figure 5.2, one set is shown with light solid lines, and the other set is shown with heavy solid lines. A triangle of one set is adjacent only to triangles of the other set. This alternation requirement is mentioned in Section 5.2 and here means only geodesic subdivisions of the octahedron can be used. The tetrahedron and icosahedron are excluded since their odd three- and five-fold symmetries don't permit the required alternating classification of the triangles. The exclusive use of the octahedron makes the computational work simpler since, as mentioned in Section 2.3, the symmetries of the octahedron are very easily expressed in the Cartesian framework.
Here both the inwardly- and outwardly-pointing t-polypods mentioned in Section 5.2 are t-tripods. The placement of the struts is chosen to maximize the untwisting effect mentioned in Section 5.2. It differs from the usual way of threading struts between adjacent triangles in single layer tensegrities.
The truss is shown graphically in Figure 5.5. The fact that only t-tripods appear in the structure gives the struts more effectiveness. They overlap less than they would if there were t-polypods of greater frequency, so the set of struts covers more area. Since the struts will in general be the most expensive component, this is a desirable feature. Also, having t-tripods everywhere rather than higher-frequency t-polypods enhances the stiffness of the structure since triangles can't distort like other polylaterals.
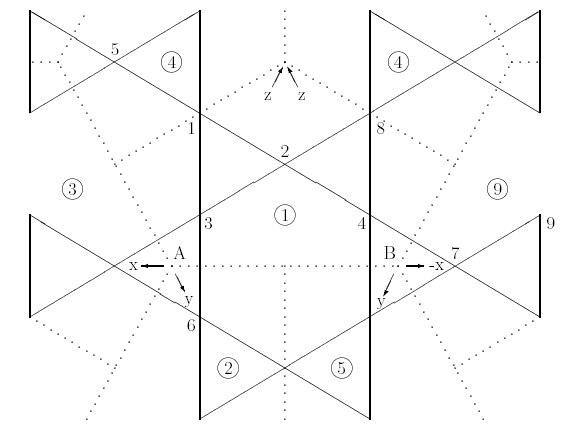 Figure 5.3: 4ν T-Octahedron Sphere: Symmetry Regions |
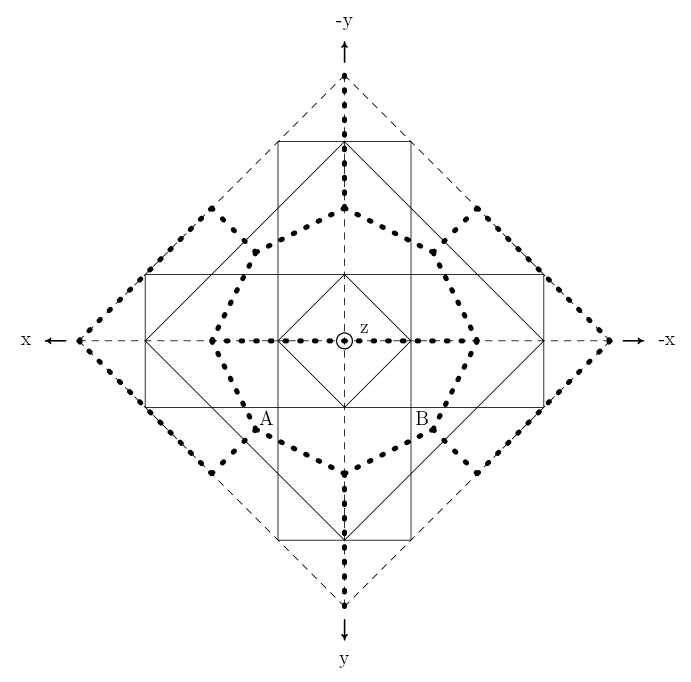 Figure 5.4: 4ν Octahedron: Double-Layer Symmetry Regions |
Figure 5.3 is a schematic which shows the identity symmetry region corresponding to the structure along with portions of the other symmetry regions that surround it. Figure 5.4 shows how the symmetry regions appear when drawn on the base octahedron. The borders of the symmetry regions appear as dotted lines in Figure 5.3 and Figure 5.4. The points labeled A and B correspond to the centers of two adjacent octahedral triangles. Arrows are used to indicate the coordinate axes within the context of each of these triangles. In Figure 5.3, the numbers in circles indicate the correspondence of each region to a symmetry transformation in Table 5.5, and the position of each point is labeled with its number.
Due to the alternating triangles, the symmetry region for a double-layer tensegrity is twice the size of that for the corresponding single-layer tensegrity. The single-layer tensegrity's symmetry region is one third of an octahedral face, so the double-layer symmetry region is the union of one third of one octahedral face with one third of an adjacent face.7
Figure 5.3 also shows visually how the point correspondences of Table 5.6 are derived. For example, is at the same position8 in symmetry region 2 as is in symmetry region 1. This means can be obtained by applying symmetry transformation 2 to .
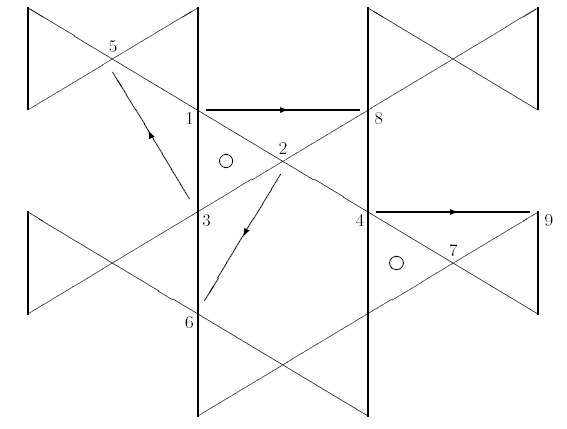 Figure 5.5: 4ν T-Octahedron Sphere: Truss Members |
Figure 5.5 indicates the positions of the basic struts which compose the structure. An arrow in the center of each strut indicates the direction from the strut's outer point to its inner point. These struts are clustered around two basic t-tripods whose centers are indicated with circles.
Table 5.1 enumerates the members of this structure. The end points of each member are shown along with its weight (if it will appear in the objective function) or its length (if it is a constraint). Outer points are indicated with the same labels as the corresponding inner points except that the labels of the outer points have a prime mark.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5.1: 4ν T-Octahedron: Truss Members |
The inner and outer tendon networks are generated by projecting the alternating triangles of Figure 5.2 onto concentric spheres. This allows Kenner's tables9 to be used to generate initial point coordinates. The radius of the inner network (2.0) is chosen so that the inner tendon lengths are all approximately 1.0, and the radius of the outer network (4.0) is chosen to yield strut lengths of approximately 3.0. Since this tensegrity doesn't share the mirror symmetry of geodesic structures, Kenner's table has to be expanded by rotating all the points about the axis by 90°. This corresponds to increasing the value of what is there called (here it is called in accordance with standard practice) by 90°.
Table 5.2 outlines the correspondence between the basic points and Kenner's coordinate system. Rotated points are indicated with an asterisk. The resulting coordinate values for the inner and outer points are summarized in Table 5.3. The realized initial lengths are summarized in Table 5.4.
| ||||||||||||||||||||||||||
|
Table 5.2: 4ν T-Octahedron: Angular Point Coordinates |
| ||||||||||||||||||||||||||||||||||||||||||
|
Table 5.3: 4ν T-Octahedron: Initial Basic Point Coordinates |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5.4: 4ν T-Octahedron: Initial Member Lengths |
The symmetry transformations for any double-layer t-octahedron are enumerated in Table 5.5. It shows how the coordinates of a symmetry point are derived from those of a basic point under each possible transformation. The derivation of the symmetry points from the basic points is shown in Table 5.6. Outer points follow the same symmetries as inner points.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5.5: T-Octahedron: Symmetry Transformations |
| ||||||||||||||||||||||||||||||||||||||||||
|
Table 5.6: 4ν T-Octahedron: Symmetry Point Correspondences |
The strategy for computing the structure is to minimize a weighted10 combination of the interlayer and binding tendons subject to constraints on the lengths of the struts and convergence tendons. An initial iteration is done using the penalty formulation in conjunction with PARTAN since an exact approach would have had difficulty given the divergence between the initial values and the constraints. After this four iterations are done with the exact formulation in conjunction with PARTAN to bring the values to convergence. The derivatives of the objective function with respect to the independent coordinate values are all less than . The independent coordinates are , , , , , , , , , , and .
Table 5.7 shows the values for the final lengths and relative forces;11 Table 5.8 shows the final values for the coordinates of the basic points, and Figure 5.6 shows the final design. This design has some interference problems which are examined and fixed in Section 8.2.3.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5.7: 4ν T-Octahedron: Final Member Lengths and Forces |
| ||||||||||||||||||||||||||||||||||||||||||
|
Table 5.8: 4ν T-Octahedron: Final Basic Point Coordinates |
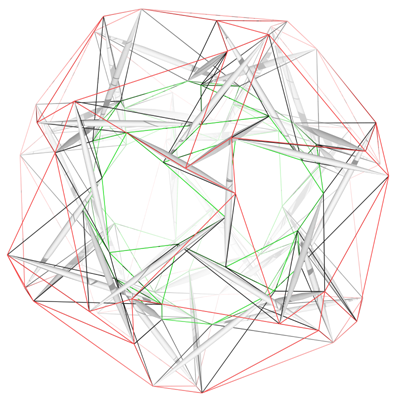 Figure 5.6: 4ν T-Octahedron Sphere: Final Design |
6 See Kenner76, Chapter 7, for a discussion of Class I and Class II subdivisions.
7 The symmetry region for a geodesic is one sixth of an octahedral face since geodesics also exhibit reflective symmetry while single-layer tensegrities based on geodesic subdivisions don't.
8 In Figures 5.3 and 5.5, 6 rather than is used to mark the position of since it marks the position of both and .
9 Kenner76, "Octahedron Class I Coordinates: Frequencies 8, 4, 2", column 4ν, p. 128.
10 The weights used are shown in Table 5.1.
11 See Section 7.2 for the method of computing relative forces.
Table of Contents
5.4 Double-Layer Tensegrities:
Hexagon/Triangle Networks