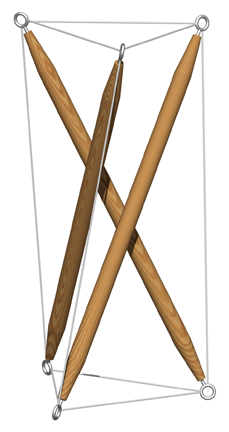
Figure 2.1: Tensegrity Prism
A Practical Guide to Tensegrity Design
Table of Contents
2.1 Basic Tensegrity Structures: Introduction
2.2 T-Prism: The Simplest Tensegrity
2.2.1 T-Prism Intuition
 Figure 2.1: Tensegrity Prism |
The t-prism is illustrated in Figure 2.1. It is the simplest and therefore one of the most instructive members of the tensegrity family. Some art historians believe it was first exhibited by the Latvian artist Karl Ioganson in Moscow in 1920-21 though this claim is controversial.1
A model can be easily constructed using 5/16-inch-diameter (8 mm) dowel, some small screw eyes,2 and some braided Dacron or nylon fishing line. The dowel should be cut into three seven-inch (178 mm) lengths and an eye screwed into either end of each length. Both eyes on a dowel should face the same direction. Then, using the fishing line, the three dowels are tied together by connecting one end of each of them to one end of each of the others so that there is a three-inch (76 mm) length of line between each pair of dowels.3 The result should be an equilateral triangle of tendons, each three inches (76 mm) long, connecting the three struts together. Next the opposite ends of the struts are tied together in a similar manner. These two sets of tendons are the end tendons. At this point, the result should be a triangular prism whose side edges are marked out by the struts and whose triangular ends are made of fishing lines (see Figure 2.2).
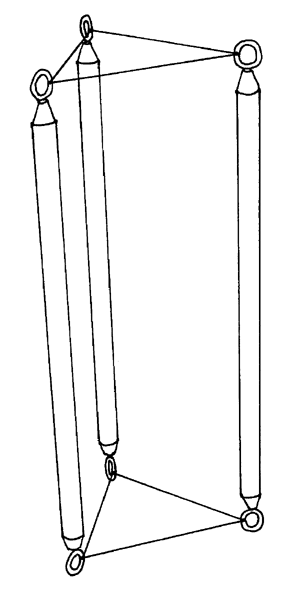 Figure 2.2: T-Prism Construction: Triangular Prism Stage |
The structure can be held up with a thumb and two fingers from each hand so that it can be viewed as a prism. When one end of the prism is twisted relative to the other, the rectangular sides of the prism lose their rectangularity and become non-planar quadrilaterals. Two opposite angles of each quadrilateral become obtuse (greater than 90°), and two opposite angles become acute (less than 90°). The structure is completed by connecting the vertices of each quadrilateral corresponding to the two obtuse angles with a tendon made of fishing line.
The length of these final three tendons (one for each side of the prism -- the side tendons) has to be chosen carefully; otherwise, the structure will turn out to be a loose jumble of sticks and fishing line. As the two ends of the prism are twisted relative to each other, the vertices corresponding to the opposite obtuse angles initially grow closer to each other. As the twisting continues, there comes a point where they start to move apart again. If the side tendons are tied with a length of fishing line which corresponds to the minimum length reached at this point,4 the structure is stable since it can't move away from that configuration except by lengthening the distance between those two points, and that is prevented by the minimum-length tendon. This is the "trick" which underlies all the tensegrity design methods explored here.
So next the computation of the length of this minimum-length tendon is explored.
2.2.2 T-Prism Mathematics: Cylindrical Coordinates
[A lot of the analysis presented in this section is derived from Kenner76, pp. 8-10. The analysis presented there is a more general one.]
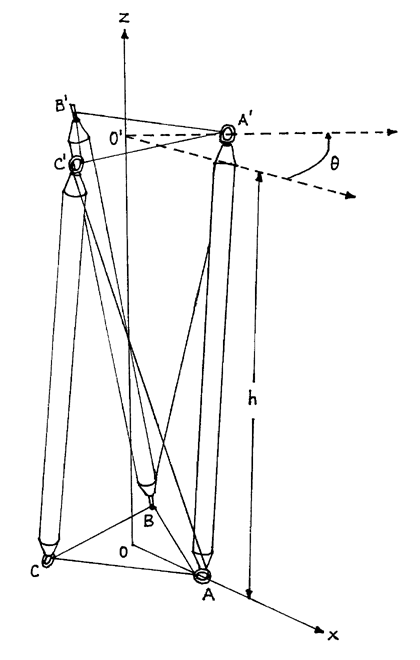
Figure 2.3: T-Prism: Cylindrical Coordinates |
For the t-prism, the most intuitive and convenient coordinate system for mathematical analysis is the cylindrical coordinate system.5 Figure 2.3 outlines how the t-prism is oriented in this system. The axis of the system coincides with the axis of the t-prism () and therefore pierces the centers of the two triangular ends. The center of one of these ends () coincides with the origin, while the other center () lies on the positive axis. The points which make up the triangle about the origin are marked with the labels , , and . The coordinate of all these points is 0. Their positions are held constant in the mathematical analysis. On the other triangle, the corresponding points are marked , and . The coordinate of these points is , the height of the t-prism. This height is a variable in the mathematical analysis.
Since the axis goes through the centers of both triangles, their vertices are equidistant from the axis. The measure of this distance, denoted , represents the radial portion of their coordinate representation. This value is also held constant for the purposes of the mathematical analysis. Besides the axis, the figure also contains the reference axis labeled . This axis serves as the reference for the value of the angular coordinate.6 The value of this coordinate for is the variable , while the value of this coordinate for is fixed at 0. The value of (which is measured in radians) measures the twist of the two triangular ends with respect to each other. Since , , and lie on the same triangle, the angular component for is and that for is . Table 2.1 summarizes the coordinate values for the six points.
| ||||||||||||||||||||||||||||||||
|
Table 2.1: T-Prism: Cylindrical Coordinates | ||||||||||||||||||||||||||||||||
Now the struts, the compressive component of the structure, can be inserted into the model. These correspond to the line segments , and . Next, the side tendons are specified to link up the two tendon triangles which make up the ends of the prism. Starting from point , the side tendon can be connected to either or . Either decision would result in a viable structure provided the connections are made consistently around the structure. One of these structures would be the mirror image of the other. Here the side tendon is connected to , so the side tendons correspond to the line segments , and .
Now the essence of the problem is reached: how long should each member (each tendon and each strut) be? By fixing the value of (the radius of the prism's triangular ends), the length of each end tendon (call this value ) has been fixed via the equation . For the other members, there are two choices. The side tendon lengths, etc., can be fixed and then etc. chosen to be the maximum-length struts compatible with these fixed tendon lengths; or, the strut lengths, etc., can be fixed and then etc. chosen to be the minimum-length side tendons compatible with these fixed strut lengths. Here, the second procedure is used.7 The choice is arbitrary, and, in this case, there is no real benefit to doing it one way or the other. In more complex structures, however, fixing the strut lengths a priori allows the designer to specify them all to be equal. This uniformity eases the manufacture of the struts since only one length of strut needs to be made.
So the problem is:
Using the variables and , minimize side tendon length keeping in mind the following constraints:
The symmetry constraints stem from the fact that this tensegrity is based on a triangular prism which exhibits three-fold symmetry about its axis. Symmetrical struts are chosen to be of equal length for convenience. They could just as well be specified to all have different lengths. The side tendon lengths are chosen to be equal for convenience also. Here more care needs to be taken since the side tendon lengths, etc., are variables of the problem, and artificial constraints here could invalidate the mathematical model of the structure. There is nothing in the geometry of the structure which says these tendons must be equal, and actually, even with all the strut lengths equal, a valid structure could be constructed with these tendons unequal in length; but, as it turns out, when the structure otherwise exhibits a rotational symmetry, imposing this symmetry on the solution results in a viable structure, and, as important, it whittles down the size of the problem considerably.
To get mathematical formulas for the different lengths, the formula for the length of a chord on a cylinder is needed. It is:
where:
|
|
Notice that the formula is expressed in terms of the second power of the length. The second root of this expression would also yield a formula for the length; but, it is just as valid,8 and, more importantly, mathematically easier, to work in second powers. In virtually every tensegrity problem examined in these notes, working with second powers of lengths makes the problem more tractable.
All this considered, the final mathematical form for the problem is:
This constrained optimization problem can be turned into an easier unconstrained one by solving the constraint for and substituting this into the objective function. Doing this, the equivalent unconstrained problem is obtained:
Taking the derivative with respect to and equating the result to 0 yields:9
or
The sines of two angles can be equal only if either their difference is an even multiple of , or their sum is an odd multiple of . In this case only the latter is a possibility.10
The first alternative is that that the sum is just , i.e. that:
which means a solution to the problem is
.
Substitution of this value for into the modified objective function above yields:
.
In the experiment above, the fixed strut length, , was and the fixed end tendon length, , was . Hence:
and therefore:
So = 6.2135 inches (158 mm).
The next alternative is that the sum is , i.e. that
This alternative yields the solution
.
This solution corresponds to a maximum value of the objective function rather than a minimum. Mathematically, this alternative could be eliminated by examining the second-order conditions for a minimum. The previous solution would fulfill them; this solution would not. For now, such care need not be taken since it is also known that needs to be positive. However, as the models get more complex, these issues need to be dealt with. This latter solution would be a valid tensegrity solution if the strut length were being maximized with respect to a fixed-length side tendon.
All other alternatives11 are equivalent to the two examined since the other alternatives can be reduced to one of the solutions examined plus an even multiple of .
2.2.3 T-Prism Mathematics: Cartesian Coordinates
As an introduction to the material presented in succeeding chapters, the triangular t-prism is re-examined from the vantage point of Cartesian coordinates. The three-fold symmetry of the triangular prism make this analysis much simpler as compared with prisms of higher symmetry.
Now each vertex of the prism is expressed as a point in -space. The three-fold symmetry constrains the coordinates of the three points within each triangle to be permutations of each other. and are arbitrarily chosen to be the basic points. The other points are called symmetry points since they are generated from the basic points via symmetry transformations, permutations in this case. These coordinate values are summarized in Table 2.2 and illustrated in Figure 2.4.
| ||||||||||||||||||||||||||||||||
|
Table 2.2: T-Prism: Cartesian Coordinates | ||||||||||||||||||||||||||||||||
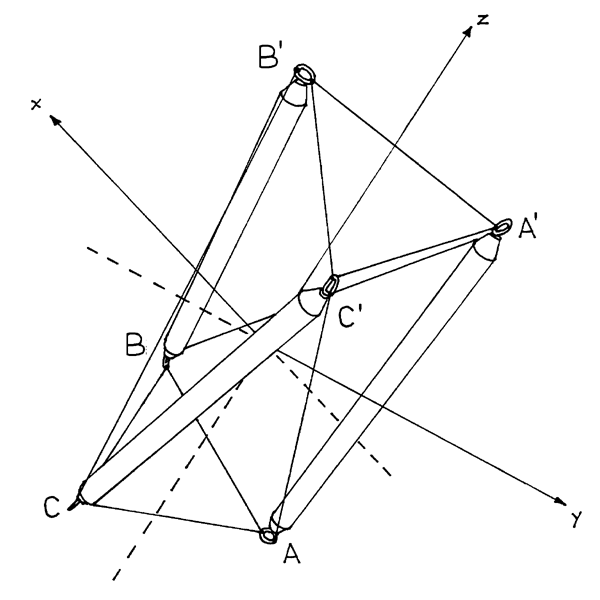 Figure 2.4: T-Prism: Cartesian Coordinates |
With Cartesian coordinates, it is no longer convenient to deal with the parameter , and instead the common length of each end tendon, , is used directly. The constraints imposed by the specification of fixed lengths for the sides of the triangles formed by the end tendons must now be explicitly written out for each triangle:
Only the constraint for one side of each triangle is written out since the symmetry of the structure (which is subsumed in the coordinate representation) ensures that if the constraint is met for one side of the triangle, the other sides satisfy the constraint also. The constraint imposed by the strut length appears as:
Again, this equation is not written out for all three struts since the structure's symmetry ensures that if the constraint is met for one strut, it is met for the others.
Taking all this into consideration, the mathematical representation of the problem now appears as:
The final two constraints are added for computational reasons. Without these constraints, the problem has infinitely many solutions.12
These equations don't lend themselves to the easy substitutions that the previous set up did, and, in this problem, certainly the previous approach is to be preferred since it is so simple to solve. The problem with the earlier approach is that it doesn't generalize as easily to more complex problems as this Cartesian approach does.
Given the complexities involved in solving a system like this, the discussion of how the solution is obtained is deferred until later when the problems absolutely require it.
2.2.4 T-Prism Mathematics: Further Generalizations
Kenner76 shows how the formulae of Section 2.2.2 can be generalized to handle four-fold and higher-symmetry prisms and cases where the radii of the ends differ. For the higher-symmetry prisms, it is also not necessary that the side tendon be restricted to connecting adjacent struts: it can skip over one or more struts in its trip from one end of the prism to the other. Although Kenner76 doesn't explore this possibility, it is easy enough to generalize his formulae to handle it.
1 Gough98, Fig. 13, p. 106, shows a tensegrity prism which claims to be a modern reconstruction of Ioganson's sculpture which was destroyed in the mid-1920's by the Soviet regime. Kenneth Snelson does not believe such a reconstruction is credible based only on the old exhibition photo which is of poor quality (see Gough98, Fig. 2 and Fig. 9, where the structure is labeled "IX" at its base). In his view, only someone who already knew about tensegrity prisms could make such a reconstruction; the necessary connections are not evident from the photo itself.
Snelson's observations seem correct, but the apparent equal lengths of the two readily visible struts, the consistency of the apparent trajectory of the less visible one with a 30° twist, and the improbability of being able to configure the struts the way they are with another arrangement of tendons would seem to point to Ioganson's priority here. That being said, the prism does not catch the imagination the way Snelson's X-Piece does. No floating of struts is readily observable. So even if priority is granted to Ioganson here, it would still seem the step to a structure like Snelson's is a significant one, even if considered as only an outgrowth of the prism which of course it was not.
As was noted in Section 1.3, the tensegrity prism was the first tensegrity structure assembled by Emmerich in 1958. It appears as Fig. 1 in his French Patent No. 1,377,290. It also appears as Fig. 22b in Snelson's U.S. Patent No. 3,169,611, but only as prior art. In the U.S., the tensegrity prism was apparently developed shortly after Snelson's X-Piece revelation since John Moelman's Tensegrity Vector Equilibrium (see Fuller73, Fig. 271), developed in 1951, is clearly two prisms bonded end-to-end.
2 Small screw eyes, 7-8 mm in diameter, work the best. Likely candidates can be found in hardware stores or picture framing shops. Anthony Pugh (Pugh76, p. 72) favors nails instead of screw eyes. Nails have the advantage that ad hoc adjustments of the member lengths don't have to be made to accommodate the dimensions of the attachment point. Pugh's detailed information on tensegrity model construction is recommended reading.
3 A stunsail tack bend (used in sailing) is an effective knot in this application. If problems are encountered tying the fishing line to the right length, thin-gauge wire can be used. This doesn't have to be knotted but merely twisted at the right length. The sharp wire ends can be a hazard.
4 The minimum is obtained when the two ends are twisted 150° relative to each other.
5 A presentation of this system can be found in most calculus texts, for instance Leithold72, p. 863.
6 The value can be expressed in radians or degrees. Here, for mathematical convenience, radians are primarily used.
7 This is implicitly the solution sought in the experiment with the t-prism carried out above. The struts were fixed in length and the t-prism was twisted until the opposite rectangle ends were as close together as possible.
8 For example, instead of constraining the strut length to be a certain value, the second power of the strut length can be constrained to the the second power of that certain value, and the effect of the constraint is the same.
9 Here an important mathematical advantage of expressing the angular measures in terms of radians is realized: the derivative of is simply . The result is equated to 0 since that is a necessary first-order condition for a minimum.
10 The difference between the two angles in question is and that for is which is not an even multiple of .
11 These would involve substituting other odd multiples of besides and into the equations above.
12 The fourth constraint requires the base of the t-prism to fall in a fixed plane orthogonal to the vector . The fifth constraint fixes the t-prism with respect to rotations about its central axis.