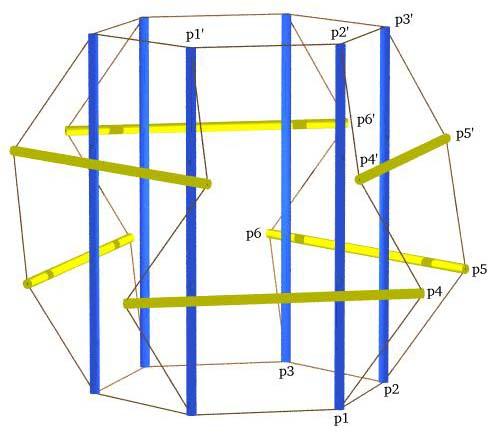
Orthogonal Girdled Six-fold Prism with Point Labels
(NB: The end1c and end2c tendons are not present in the diagram
but are essential for the stability of the sculpture.)
(VRML Model)
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# struts
<Member> strut1a p2' p1 0.0
sqr(cos(acos(-sqrt(3)/3) - pi/2) + sqrt(3)*cos(acos(-1/3) - pi/2))
1 Con CalcClear Inelastic *
<Member> strut1b p3' p2 0.0
sqr(cos(acos(-sqrt(3)/3) - pi/2) + sqrt(3)*cos(acos(-1/3) - pi/2))
1 Con CalcClear Inelastic *
<Member> strut2a p4' p5' -1.0 0.0 1 Obj CalcClear Inelastic *
<Member> strut2b p5 p6 -1.0 0.0 1 Obj CalcClear Inelastic *
# side tendons
<Member> side1a p4' p2' 1.0 sqr(1.0) 3 Con *
<Member> side2a p4 p4' 1.0 sqr(1.0) 3 Con *
<Member> side3a p1 p4 1.0 sqr(1.0) 3 Con *
<Member> side1b p5' p3' 1.0 sqr(1.0) 3 Con *
<Member> side2b p5 p5' 1.0 sqr(1.0) 3 Con *
<Member> side3b p2 p5 1.0 sqr(1.0) 3 Con *
# bottom tendons
<Member> end1a p2 p1 1.0 sqr(1.0) 2 Con *
<Member> end1b p3 p2 1.0 sqr(1.0) 2 Con *
<Member> end1c p3 p1 0.1 3.0 7 Con *
# top tendons
<Member> end2a p2' p1' 1.0 sqr(1.0) 4 Con *
<Member> end2b p3' p2' 1.0 sqr(1.0) 4 Con *
<Member> end2c p3' p1' 0.1 3.0 7 Con *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
screw-eye center to screw-eye center, as are the tendon lengths.
These values are in model units.
strut1a: 2.44949 strut1b: 2.44949 strut2a: 2
strut2b: 2 side1a: 1 side2a: 1
side3a: 1 side1b: 1 side2b: 1
side3b: 1 end1a: 1 end1b: 1
end1c: 1.73205 end2a: 1 end2b: 1
end2c: 1.73205
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed. The
roundness of these numbers is extraordinary.
strut1a: -1.63299 strut1b: -1.63299 strut2a: -2
strut2b: -2 side1a: 2 side2a: 2
side3a: 2 side1b: 2 side2b: 2
side3b: 2 end1a: 0.666667 end1b: 1.33333
end1c: 0 end2a: 0.666667 end2b: 1.33333
end2c: 0
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of the 5/16-inch-diameter wooden dowel.
Braided nylon fishing line was used for the tendons.
Prestress forces are assumed to affect tendon lengths and
not strut lengths.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> 0.02
Length Scale Factor> 292/2.44949
Strut and Tendon Hub Adjustments - s;t> 5.0 3.5
(The 5.0 mm adjustment for the strut is the amount
the screw-eye center extends from the dowel. The 3.5 mm
adjustment for the tendon is half the outer diameter of the
screw eye.)
strut1a: 282 0 strut1b: 282 0 strut2a: 228 1 strut2b: 228 1
side1a: 109 0 side2a: 109 0 side3a: 109 0 side1b: 109 0
side2b: 109 0 side3b: 109 0 end1a: 111 0 end1b: 110 0
end1c: 199 1 end2a: 111 0 end2b: 110 0 end2c: 199 1

Orthogonal Girdled Six-fold Prism with Point Labels
(NB: The end1c and end2c tendons are not present in the diagram
but are essential for the stability of the sculpture.)
(VRML Model)
structure file: tprism/x6girdle6.rc variable file: tprism/x6girdle6.dat digit list: ../src/mm.dls |
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com
Back to Modified Orthogonal Girdled Six-fold Prism
More Datasheets