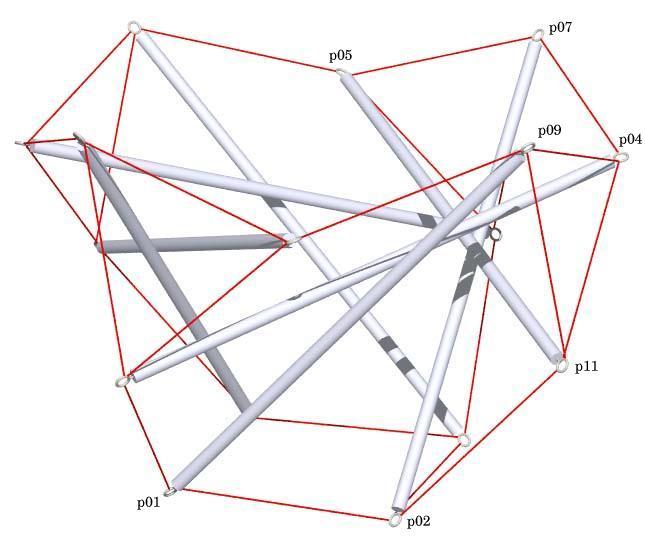
View of the Tensegrity Tulip
with Point Labels
Hub Connectivity
This shows how hub vectors (hv01.1 ...) are applied to the
strut end points (p01 ...) to derive hub points (hp01.1 ...).
Hub points are where tendons are connected to the strut.
<VecPt> hp01.1 p01 + hv01.1
<VecPt> hp01.2 p01 + hv01.2
<VecPt> hp01.3 p01 + hv01.3
<VecPt> hp05.1 p05 + hv05.1
<VecPt> hp05.2 p05 + hv05.2
<VecPt> hp05.3 p05 + hv05.3
<VecPt> hp09.1 p09 + hv09.1
<VecPt> hp09.2 p09 + hv09.2
<VecPt> hp09.3 p09 + hv09.3
<VecPt> hp11.1 p11 + hv11.1
<VecPt> hp11.2 p11 + hv11.2
<VecPt> hp11.3 p11 + hv11.3
Transformations
This shows how transforms are defined and how they are
applied to derive transformed objects from basic objects.
# rotation matrices
<XMat> x4 cos(2*pi/4) (-sin(2*pi/4)) 0 sin(2*pi/4) cos(2*pi/4) 0 0 0 1
<CompositeXform> x4^2 x4 x4
<CompositeXform> x4^3 x4 x4^2
# transform points and vectors
<XformPt> p02 p01 x4
<XformPt> hp02.1 hp01.1 x4
<XformPt> hp02.2 hp01.2 x4
<XformPt> hp02.3 hp01.3 x4
<XformPt> p04 p05 x4^3
<XformPt> hp04.1 hp05.1 x4^3
<XformPt> hp04.2 hp05.2 x4^3
<XformPt> hp04.3 hp05.3 x4^3
<XformPt> p07 p09 x4
<XformPt> hp07.1 hp09.1 x4
<XformPt> hp07.2 hp09.2 x4
<XformPt> hp07.3 hp09.3 x4
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# struts
<Member> strut1 p01 p09 0.00 sqr(317) 1 Con CalcClear *
<Member> strut2 p05 p11 0.00 sqr(317) 1 Con CalcClear *
# square tendon
<Member> sqten hp01.1 hp02.2 0.00 sqr(129.2792) 2 Con *
# triangle tendons
<Member> triten1 hp04.1 hp09.1 0.00 sqr(129.2792) 2 Con *
<Member> triten2 hp09.2 hp11.1 0.00 sqr(129.2792) 2 Con *
<Member> triten3 hp11.2 hp04.2 0.00 sqr(129.2792) 2 Con *
# zig-zag tendons
<Member> zzten1 hp02.3 hp11.3 1.00 0.00 3 Obj *
<Member> zzten2 hp04.3 hp07.3 1.00 sqr(129.2792) 3 Con *
Hub Constructs
These items are just vectors corresponding to each of the
struts. At some point the software will be modified so
these items aren't necessary since it should be possible
to treat any member as a vector without explicit constructs.
<DiffVec> strut1v p01 p09
<DiffVec> strut2v p05 p11
Hub Constraints
These are constraints the hub vectors must meet. For
these constraints to be specified, a set of
center vectors (cv01, ...) is introduced. There is one
center vector for each strut end point. The center vectors
are constrained to be orthogonal to the strut. For each
tendon connected to a strut end point, there is a hub
vector. All the hub vectors at a strut end point must
be orthogonal to the corresponding center vector and
4 mm long. 4 mm is the outer radius of the screw eye.
The center vectors are constrained to be of length one
just to make their values well defined.
<VecDotVec> hubdot01 strut1v cv01 1.0 0.0 Con
<VecLength> cvlen01 cv01 1.0 sqr(1.0) Con
<VecDotVec> hubdot01.1 cv01 hv01.1 1.0 0.0 Con
<VecDotVec> hubdot01.2 cv01 hv01.2 1.0 0.0 Con
<VecDotVec> hubdot01.3 cv01 hv01.3 1.0 0.0 Con
<VecLength> hvlen01.1 hv01.1 1.0 sqr(4.0) Con
<VecLength> hvlen01.2 hv01.2 1.0 sqr(4.0) Con
<VecLength> hvlen01.3 hv01.3 1.0 sqr(4.0) Con
<VecDotVec> hubdot09 strut1v cv09 1.0 0.0 Con
<VecLength> cvlen09 cv09 1.0 sqr(1.0) Con
<VecDotVec> hubdot09.1 cv09 hv09.1 1.0 0.0 Con
<VecDotVec> hubdot09.2 cv09 hv09.2 1.0 0.0 Con
<VecDotVec> hubdot09.3 cv09 hv09.3 1.0 0.0 Con
<VecLength> hvlen09.1 hv09.1 1.0 sqr(4.0) Con
<VecLength> hvlen09.2 hv09.2 1.0 sqr(4.0) Con
<VecLength> hvlen09.3 hv09.3 1.0 sqr(4.0) Con
<VecDotVec> hubdot05 strut2v cv05 1.0 0.0 Con
<VecLength> cvlen05 cv05 1.0 sqr(1.0) Con
<VecDotVec> hubdot05.1 cv05 hv05.1 1.0 0.0 Con
<VecDotVec> hubdot05.2 cv05 hv05.2 1.0 0.0 Con
<VecDotVec> hubdot05.3 cv05 hv05.3 1.0 0.0 Con
<VecLength> hvlen05.1 hv05.1 1.0 sqr(4.0) Con
<VecLength> hvlen05.2 hv05.2 1.0 sqr(4.0) Con
<VecLength> hvlen05.3 hv05.3 1.0 sqr(4.0) Con
<VecDotVec> hubdot11 strut2v cv11 1.0 0.0 Con
<VecLength> cvlen11 cv11 1.0 sqr(1.0) Con
<VecDotVec> hubdot11.1 cv11 hv11.1 1.0 0.0 Con
<VecDotVec> hubdot11.2 cv11 hv11.2 1.0 0.0 Con
<VecDotVec> hubdot11.3 cv11 hv11.3 1.0 0.0 Con
<VecLength> hvlen11.1 hv11.1 1.0 sqr(4.0) Con
<VecLength> hvlen11.2 hv11.2 1.0 sqr(4.0) Con
<VecLength> hvlen11.3 hv11.3 1.0 sqr(4.0) Con
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
screw-eye center to screw-eye center. The tendon lengths
are from screw-eye rim to screw-eye rim. Since the model
has been scaled appropriately, these values are in millimeters.
strut1: 317 strut2: 317 sqten: 129.279
triten1: 129.279 triten2: 129.279 triten3: 129.279
zzten1: 129.279 zzten2: 129.279
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
strut1: -129.702 strut2: -133.842 sqten: 79.7366
triten1: 83.7261 triten2: 32.1339 triten3: 150.757
zzten1: 129.279 zzten2: 135.186
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of the wooden dowel. Prestress forces
are assumed to affect tendon lengths and not strut lengths.
Here no ad hoc adjustment is necessary for the tendons since
the hubs are included explicitly in the mathematical
programming problem.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> 0.02
Length Scale Factor> 1.0
(Things are scaled so model and construction units are the same.)
Strut and Tendon Hub Adjustments - s;t> 6.5 0
(Hub connections were handled explicity in the mathematical
programming problem, so no ad hoc adjustment is needed here
to account for the tendon hub connections. The 6.5 mm
adjustment for the strut represents the amount the
screw-eye center extends from the dowel.)
strut1: 304 0 strut2: 304 0 sqten: 127 1
triten1: 127 0 triten2: 128 1 triten3: 125 1
zzten1: 126 0 zzten2: 126 0
Construction Lengths -- ad hoc adjustment
For comparison, these are the construction lengths computed
from the model where all members are assumed to meet
at a single point and a simple ad hoc adjument is applied
to account for hub geometry. If the the ad hoc adjustment
is working well, the values here should be the same as the
ones above. All the tendon values are 0.5 mm off, which is
within assembly tolerances. This is good, because it means
the ad hoc adjustment works. It is much easier to do the
ad hoc adjustment than to model the hubs explicitly.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 317/2.31755
Strut and Tendon Hub Adjustments - s;t> 6.5 4.0
(The 6.5 mm adjustment for the strut is the amount
the screw-eye center extends from the dowel. The 4 mm
adjustment for the tendon is half the outer diameter of the
screw eye.)
strut1: 304 0 strut2: 304 0 sqten: 127 0
triten1: 126 1 triten2: 128 0 triten3: 125 0
zzten1: 125 1 zzten2: 125 1

View of the Tensegrity Tulip
with Point Labels
structure files: flower/x4flower1.rc (ad hoc)
flower/x4flower1c.rc (exact)
variable files: flower/x4flower1.dat
flower/x4flower1c.dat
digit list: src/mm.dls
|
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com