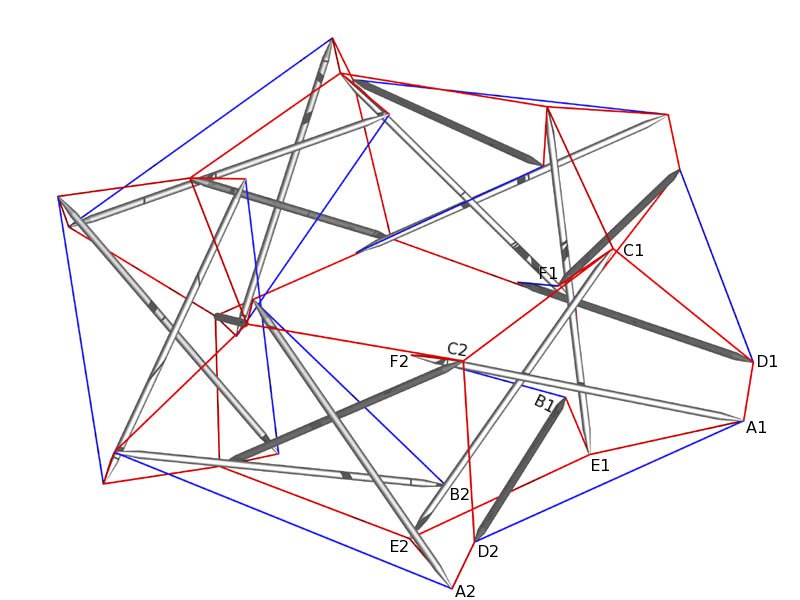
Second Wheel Based on Gůmez JŠuregui Module with Point Labels
structure file: val/bridge1c.rc
variable file: val/bridge1c.dat
digit list: src/mm.dls
|
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# struts
<Member> sA1F2 A1 F2 -1.0 sqr(14) 1 Con CalcClear *
<Member> sB1D2 B1 D2 -1.0 sqr(14) 1 Con CalcClear *
<Member> sC1E2 C1 E2 -1.0 sqr(14) 1 Con CalcClear *
# tendons
<Member> tA1D1 A1 D1 2.0 sqr(2.60000) 2 Con *
<Member> tA1D2 A1 D2 1.0 sqr(14) 3 Con *
<Member> tA1E1 A1 E1 1.0 sqr(7.06508) 2 Con *
<Member> tB1E1 B1 E1 1.0 sqr(2.58990) 2 Con *
<Member> tB1F2 B1 F2 1.0 sqr(10.0000) 3 Obj *
<Member> tC1C2 C1 C2 1.0 sqr(8.500) 2 Con *
<Member> tC1D1 C1 D1 1.0 sqr(7.06508) 2 Con *
<Member> tC1F1 C1 F1 1.0 sqr(2.58990) 2 Con *
<Member> tE1E2 E1 E2 1.0 sqr(8.500) 2 Con *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from pin insertion
point to pin insertion point, as are the tendon lengths.
The values are in model units.
sA1F2: 14 sB1D2: 14 sC1E2: 14
tA1D1: 2.6 tA1D2: 14 tA1E1: 7.06508
tB1E1: 2.5899 tB1F2: 10.9856 tC1C2: 8.5
tC1D1: 7.06508 tC1F1: 2.5899 tE1E2: 8.5
Relative Member Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
sA1F2: -12.791 sB1D2: -12.791 sC1E2: -10.0178
tA1D1: 7.39343 tA1D2: 8.26589 tA1E1: 7.71797
tB1E1: 7.50644 tB1F2: 10.9856 tC1C2: 5.57822
tC1D1: 7.71797 tC1F1: 7.50644 tE1E2: 5.57822
Average tendon force magnitude: 7.58335
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of the 3/16-inch-diameter wooden dowel.
The tendons were made of 12-lb.-test braided nylon fishing line.
In this case, the attachment point at the hubs was a simple
metal pin stuck into the end of the strut, so no member-length
adjustments were necessary. Prestress forces are assumed
not to affect strut lengths.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 150/14
Strut and Tendon Hub Adjustments - s;t> 0 0
sA1F2: 150 0 sB1D2: 150 0 sC1E2: 150 0 tA1D1: 27 1
tA1D2: 147 0 tA1E1: 74 0 tB1E1: 27 0 tB1F2: 114 1
tC1C2: 90 0 tC1D1: 74 0 tC1F1: 27 0 tE1E2: 90 0

Second Wheel Based on Gůmez JŠuregui Module with Point Labels
structure file: val/bridge1c.rc
variable file: val/bridge1c.dat
digit list: src/mm.dls
|
|
CONTACT: Bob Burkhardt Tensegrity Solutions Box 426164 Cambridge, MA 02142-0021 USA e-mail: bobwb@juno.com |
Back to
Two Wheels Based on Gůmez JŠuregui Module
More Datasheets