Receipt of eight-way D-Stix connectors allowed me to expand my horizons modestly beyond the 4ν Tetrahedral Geodesics of the previous photo to the thirteen great circles of the tetrahedron and the octahedron. My curiousity had been aroused after contemplating the 4ν Class I Tetrahedral Geodesic which clearly exhibited many great circles. Fuller doesn't dwell on this complex of great circles preferring instead to lavish attention on the 25 great circles of the vector equilibrium (see Synergetics, Fig. 454.06) and the 31 great circles of the icosahedron (see Fig. 457.40). Those figures had nodes that were way beyond the capacity of my D-Stix connectors however.
I also think the simpler 13-circle complex associated with the tetrahedron and octahedron serves as a more approachable introduction to Fuller's treatment of symmetry in terms of great circles rather than the symmetry-axis approach I was used to. With his approach, the representation of rotational and reflective symmetry is uniform: a rotational symmetry is represented by the great circle corresponding to the axis of rotation; a reflective symmetry is represented by the great circle in the plane of reflection.
Hugh Kenner's Geodesic Math (now back in print!) treats "Great-Circle Systems" on pp. 50-53. However there too the concentration is on the great circles of the icosahedron. Systems for the tetrahedron and octahedron are only briefly mentioned. The discussion of the tetrahedron has two errors: the six circles associated with reflective symmetries of the tetrahedron are left out, and the circles associated with pairs of edges are miscounted as four instead of three. For this reason, Kenner doesn't realize that the systems for both tetrahedron and octahedron are equivalent and have 13 circles.
All the tensegrity viewers have an entry for "Thirteen Great Circles" and a color ray-trace of the system is below. The octahedron appears in black. Its dual, the cube, appears in blue. The vector equilibrium appears in white. Its dual, the rhombic dodecahedron, appears in red. You can also trace out a tetrahedron in red if you look carefully: each face is made up of three faces of the rhombic dodecahedron. If you look even more carefully, you will notice that the rhombic dodecahedron can be decomposed into two intersecting tetrahedrons which together stabilize the cube. Looking at the projection of polyhedra onto spheres was also something Fuller's work introduced to me.
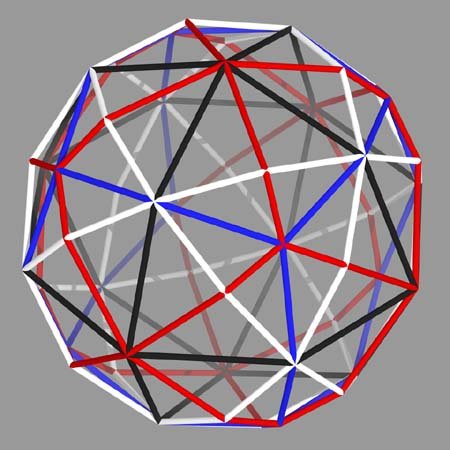
Color Key to the Thirteen Great Circles
I assembled the model on September 16, 1981, and reassembled it on December 26, 2005. The year before the reassembly I had recorded some of the insights from contemplating this system in Parable of the 13 Great Circles. The 13 circles can be inventoried as follows:
| Octahedron | Tetrahedron | Count |
|---|---|---|
| Pairs of opposite vertices | Pairs of opposite edges | 3 |
| Pairs of opposite edges | Midpoint of edge paired with opposite edge -- defines a plane of reflective symmetry | 6 |
| Pairs of opposite faces | Vertex paired with opposite face | 4 |
| Total | 13 | |
Buckminster Fuller's first geodesic domes were made completely with great circles like this. Very quickly he realized that just subdividing triangles of the base polyhedra was more effective. Geodesic was completely appropriate as a label for those earliest domes: a great circle arc is the shortest distance between two points on a sphere and hence is mathematically termed a geodesic. Even in many later dome realizations there are indeed still many geodesics to be found, but they tend to be much more fragmentary and leave people wondering where the name came from.