Figure 15: Equation for Omnidirectional Closest Packing of Spheres
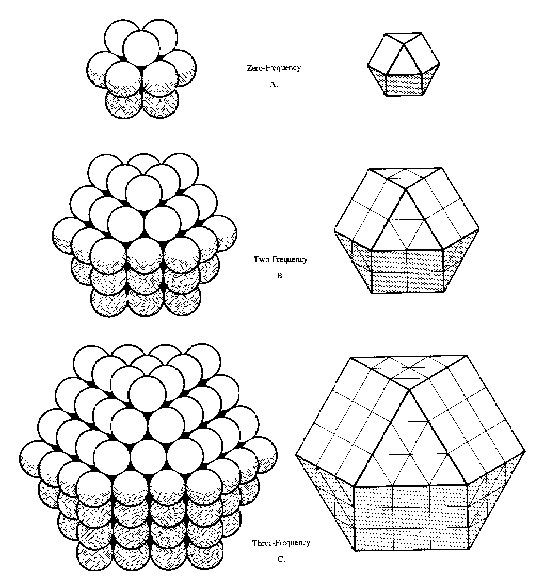

Equation for Omnidirectional Closest Packing of Spheres: Omnidirectional closest packings of equal radius spheres about a nuclear sphere form a concentric series of vector equilibria of progressively higher frequencies. The number of spheres (or, in the case of the counterpart polyvertexia, the number of edge intervals) on any symmetrically concentric shell or layer is given by the equation 10F2 + 2, where F = Frequency. The frequency can be considered as the number of layers (concentric shells or radius) or the number of edge modules on the vector equilibrium. A one-frequency sphere packing system has 12 spheres on the outer layer (A) and a one-frequency vector equilibrium has 12 vertexes. If another layer of spheres are packed around the one-frequency system, exactly 42 additional spheres are required to make this a two-frequency system (B), If still another layer of spheres is added to the two-frequency system, exactly 92 additional spheres are required to make the three-frequency system (C). A four-frequency system will have 162 spheres on its outer layer. A five-frequency system will have 252 spheres on its outer layer, etc.