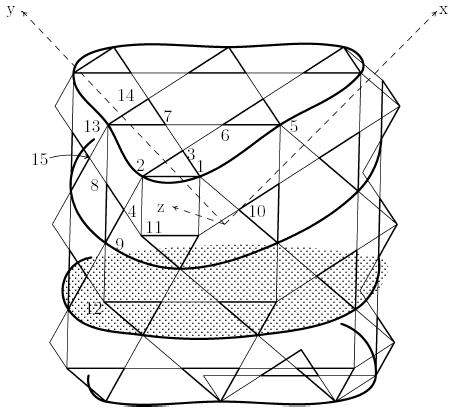
Figure 6.6: 6ν Octahedron: Unprojected Truncation Boundaries
A Practical Guide to Tensegrity Design
Table of Contents
6.2.1 Dome Step 1: Compute the sphere
6.2.2 Dome Step 2: Implement the truncation
Figure 6.6 diagrams the four "great"-circle truncation possibilities for this structure as they fall on its reference octahedron. Figure 6.7 shows the same four truncation boundaries as they fall on the inner layer of the sphere. None of these boundaries corresponds to a true great circle. The true great circle lies at the center of their range and is not usable as a truncation at this frequency. In a higher-frequency structure there would be still more of these circles available. All of them are possibilities as truncation definitions, although the ones farther away from the true great circle would probably require greater adjustments to work well. At this frequency, the two middle truncations are equally far from the true great circle, and so neither has an advantage as far as adjustments required. This being the case, the one that allows more volume is selected.
 Figure 6.6: 6ν Octahedron: Unprojected Truncation Boundaries |
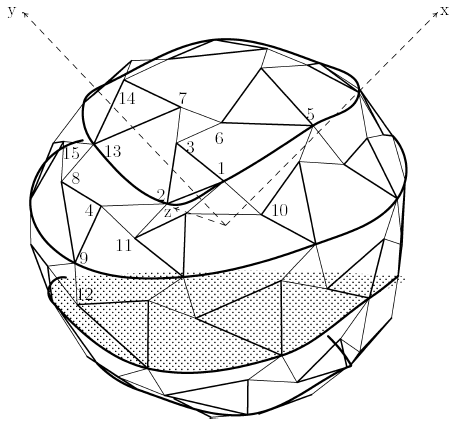 Figure 6.7: 6ν Octahedron: Projected Truncation Boundaries |
Figures 6.8 and 6.9 diagram the basic triangle network for the truncated structure and a coordinate system for its analysis. These figures are in roughly the same style as the corresponding figures for the 4ν and 6ν spheres. Figure 6.8 is more complex than for those earlier structures since it attempts to diagram the correspondence between the symmetry regions of the 6ν sphere and those of the dome.
The boundaries of the symmetry regions for the sphere are outlined with dotted lines and labeled with small numbers in circles. The numbers correspond to the symmetry transformations listed in Table 5.5. The boundaries for the dome are outlined by a hollow dotted line. The dome's symmetry regions are enumerated with larger numbers in circles. These numbers also correspond to the symmetry transformations listed in Table 5.5, although, due to the loss of symmetry, only the first three entries in the table are possibilities. A grasp of the correspondence between the symmetry regions for the sphere and those for the dome is useful for generating initial points for the dome calculations from the final values of the sphere calculations. These correspondences are used in Tables 6.16 and 6.17. As noted below, these correspondences are altered slightly for the inner points at the base of the dome.
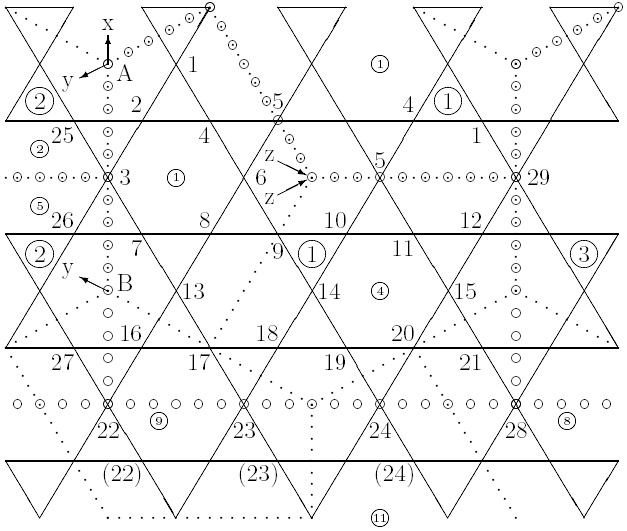 Figure 6.8: 6ν T-Octahedron Dome: Symmetry Regions |
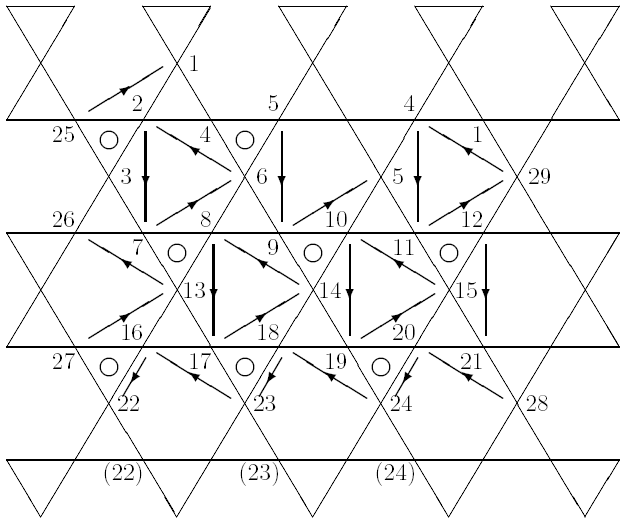 Figure 6.9: 6ν T-Octahedron Dome: Truss Members |
Tables 6.9 through 6.16 enumerate the members of the truncated structure. The anomalous members which have a length of 1.5 correspond to Member #33 in Table 6.1 for the sphere. For the most part, the weights for this structure are mapped from the weights used for the corresponding members in the spherical version of the structure. The exceptions are the weights for members #160, #161, #163, #164, #166 and #167. The reasons for these exceptions are discussed below. In addition to the members enumerated in Tables 6.9 through 6.16, guys are introduced in Step 4.
Due to the loss of symmetry induced by the truncation, the tables for the dome are much larger than for the sphere, and the computations required are correspondingly more massive. The dome is composed of three symmetrical parts whereas the same area on the sphere is composed of about eight symmetrical parts. The net result is that the tables for the dome are over twice as large as those for the sphere.
Decisions must be made in the neighborhood of the truncation on how to reroute the struts whose inner terminal points lay on the set of triangles which are excluded. The best procedure seems to be to connect them to the inner binding triangle which underlies their tripod. To make this work, the weights are multiplied by for inner binding triangle tendons which touch the base. These are the members mentioned above whose weights do not equal those of the corresponding members in the spherical structure (#160, #161, #163, #164, #166, #167). This reduction in the weights allows the final dome to achieve a height which approximates the height of its initial configuration. With unaltered weights, it would turn out more squat.
The secondary interlayer tendons at these positions, #64, #67 and #70, disappear since there are struts at those same positions in this configuration. Also, the tendons generated by the truncation are eliminated from the model. The inner truncation tendons are redundant since they connect the base points which are fixed. The outer truncation tendons are not necessary for structural integrity and detract from the appearance of the structure.
In Tables 6.9 through 6.16, members re-routed to a new inner point (as compared with the configuration of their corresponding member in the sphere) due to the truncation are marked with †. Members which are excluded (although for completeness they are included in the tables) are marked with ‡.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.9: 6ν T-Octahedron Dome: Struts |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.10: 6ν T-Octahedron Dome: Primary Interlayer Tendons |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.11: 6ν T-Octahedron Dome: Secondary Interlayer Tendons |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.12: 6ν T-Octahedron Dome: Inner Convergence Tendons |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.13: 6ν T-Octahedron Dome: Outer Convergence Tendons |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.14: 6ν T-Octahedron Dome: Outer Binding Tendons |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.15: 6ν T-Octahedron Dome: Inner Binding Tendons |
| ||||||||||||||||||||||||
|
Table 6.16: 6ν T-Octahedron Dome: Truncation Tendons |
The basic points and their initial coordinate values (as derived from the final values for the corresponding points in the sphere) are summarized in Tables 6.17 and 6.18. The applicable transforms are listed in Table 5.5. The coordinates of and do not correspond exactly to the values of the corresponding points in the sphere. This is due to the Step 3 adjustment.
, and of the truncated sphere map from , and respectively of the complete sphere, rather than , and as would be expected from an unaltered symmetry mapping. This alteration is made so that, even with the change in topology, the initial positions and lengths of the struts in the dome correspond to their final positions in the sphere computations. Since the spherical excesses of and differ from and , the initial weights for members #160, #161, #166 and #167, also differ from the values for the corresponding members of the spherical structure. In addition, as mentioned above, the actual weights used for these members, as well as those for #163 and #164, are times the weights corresponding to the sphere.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.17: 6ν T-Octahedron Dome: Initial Inner Coordinate Values |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6.18: 6ν T-Octahedron Dome: Initial Outer Coordinate Values |
The derivation of the symmetry points from the basic points is shown in Table 6.19. Outer points follow the same symmetries as inner points. As mentioned above, due to the loss of symmetry as a result of the truncation, only the first three entries of Table 5.5 are possibilities here.
| ||||||||||||||||||||||||||||||||||||||||||
|
Table 6.19: 6ν T-Octahedron Dome: Symmetry Point Correspondences |