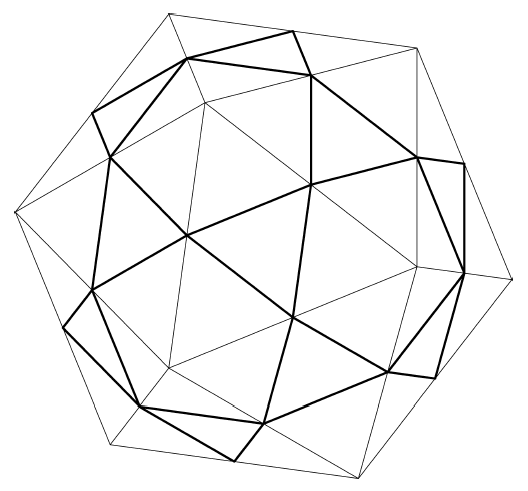
Figure 5.7: 2ν Icosahedron
A Practical Guide to Tensegrity Design
Table of Contents
5.3 Double-Layer Tensegrities:
Geodesic Networks
5.4 Double-Layer Tensegrities: Hexagon/Triangle Networks
A second approach to designing tensegrity trusses relies on networks which have triangles alternating with hexagons and pentagons, rather than triangles alternating with triangles as with the first approach. An advantage of this approach over the approach of Section 5.3 is that it works with all symmetries; in addition to Class I and Class II breakdowns of the octahedron, geodesic breakdowns of the tetrahedron and icosahedron can be used.
Geodesic networks are used here only as a first step in the derivation of a network. In the geodesic network's triangles, attention is now also placed on the hexagons which fill up the gaps between the triangles. Thus, these triangles and the gaps between them form a system of alternating triangles and hexagons except at the vertices of the base polyhedron where a triangle, square or pentagon is substituted for a hexagon.
 Figure 5.7: 2ν Icosahedron |
For an example, see Figure 5.7 which illustrates a 2ν icosahedron. At this low frequency, the single triangles on each icosahedral face surround pentagonal gaps which correspond to the vertices of the base icosahedron. At higher frequencies, hexagonal gaps would appear on the edges (as in Figure 4.2) and/or the faces of the base polyhedron. At high frequencies, the hexagonal gaps dominate since the occasional pentagonal, square or triangular gaps only appear at the vertices of the base polyhedron. Hence, the final network is referred to as a "hexagon/triangle" network even though at the lowest 2ν frequency hexagons don't appear at all.
This recontextualized geodesic network is not suitable for a t-tripod-based tensegrity truss though since adjacent polylaterals share edges rather than just points. A suitable network can easily be constructed though by inscribing a smaller version of each polylateral within that polylateral by connecting the midpoints of its sides appropriately. This technique is illustrated for the 2ν icosahedron in Figure 5.8.
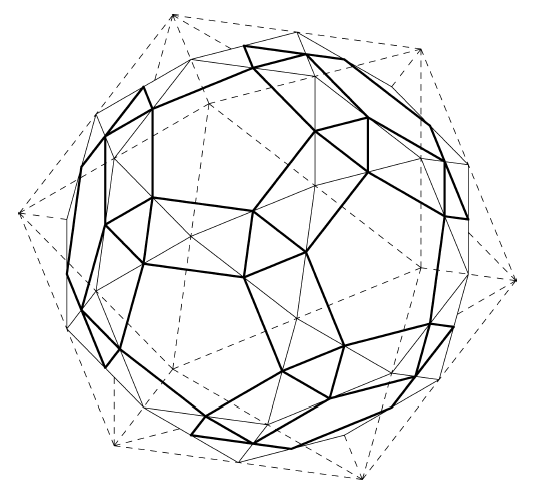 Figure 5.8: Hexagon/Triangle Tensegrity Network Inscribed in 2ν Icosahedron |
As in Section 5.3, this network is projected on a sphere and duplicated to form an inner and outer network. The triangles on the outer network form the apexes of outwardly-pointing t-tripods (the outer convergence triangles), while the hexalaterals on the outer network form the tendons which bind them together (the outer binding hexalaterals). On the inner sphere, the hexalaterals form the apexes of inwardly-pointing t-hexapods (the inner convergence hexalaterals), and the triangles form the tendons which bind them together (the inner binding triangles). The struts and their corresponding tendons (the primary and secondary interlayer tendons) connect the triangles on the outer network with the hexalaterals on the inner network. As before, struts are placed so that the untwisting effect of the binding tendons is enhanced.
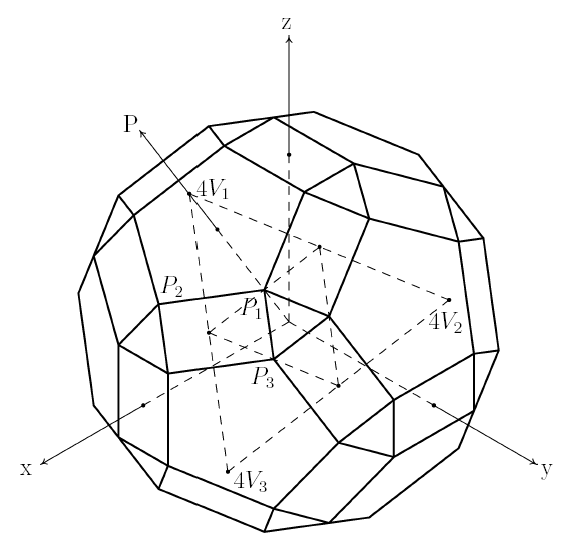 Figure 5.9: 2ν Hexagon/Triangle T-Icosahedron: Coordinate System |
Figure 5.9 illustrates this network as represented in Cartesian coordinates. This representation is meant to exploit the octahedral symmetries of the icosahedron as much as possible. Thus many of the symmetry points are simple signed permutations of the basic points. To capture the icosahedral symmetries however, a general transformation matrix must be introduced.
In Figure 5.9, the axis labeled P represents the five-fold symmetry axis about which the structure is transformed.12 This axis goes through a vertex of the reference unit-side-length icosahedron. The coordinates of this vertex are where is the ratio constant of the golden section. This transformation is needed to express in terms of the basic point .13 is generated from by a -72° rotation of the structure about the axis . The matrix which achieves this transformation is:14
Thus each coordinate of is represented as a linear combination of the coordinates of . In the model, this substitution could be made in all the formulas. However, it is simpler just to consider as a basic point and introduce the transformation matrix as three constraints expressing the coordinates of as linear combinations of the coordinates of .
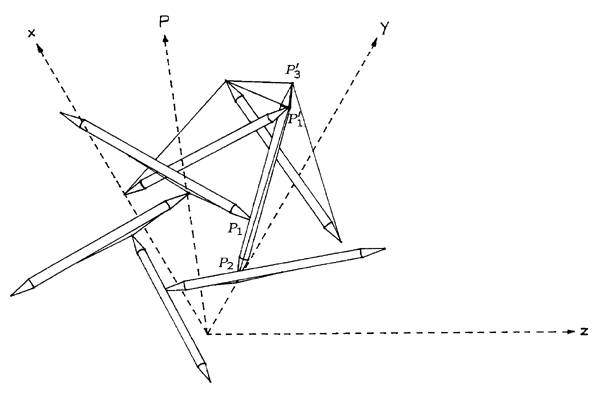 Figure 5.10: 2ν Hexagon/Triangle T-Icosahedron: Truss Members |
Figure 5.10 illustrates the basic members of the structure as well as an outline of some of the symmetry members embedded in the coordinate system which is used to analyze the structure. The low frequency of the structure means there are very few basic members to keep track of. On the other hand, the high order of symmetry of the icosahedron means that the structure as a whole will encompass about as much space as a structure based on a more complicated 4ν breakdown of the octahedron. This symmetry-induced simplicity is an important consideration in favor of icosahedral structures. Table 5.9 summarizes the member breakdown including weights for members included in the objective function and length constraints for the others.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 5.9: 2ν Hexagon/Triangle T-Icosahedron: Truss Members |
The mathematical programming problem reduces to:
The latter "two" constraints actually represent six linear constraints in all and are the icosahedral symmetry transformations.
The next thing needed is initial coordinate values for the computation. These are derived from the coordinates the unit icosahedron vertices, in particular, the coordinates of the icosahedral triangle generated by axes permutations located in the positive octant. Table 5.10 summarizes these coordinate values. The locations of , and are shown in Figure 5.9.
| ||||||||||||||||||||
|
Table 5.10: Unit Icosahedron: Selected Vertex Coordinates | ||||||||||||||||||||
Taking the midpoints of the sides of the triangle represented by these three points yields the vertices of a triangle of a half-scale version of the unit icosadodecahedron. Taking the midpoints of this second triangle and multiplying by four yields the vertices of a triangle of a unit-scale version of the the reference network for the tensegrity being analyzed here. The coordinates of the point needed are:
This serves as the initial value for . The initial value for is computed by scaling up until the strut length constraint is approximately satisfied. A value of 1.5 for the scale factor worked satisfactorily here. These initial coordinate values are summarized in Table 5.11.
| ||||||||||||||||
|
Table 5.11: 2ν Hexagon/Triangle T-Icosahedron: Initial Basic Point Coordinates | ||||||||||||||||
Since and are being treated as control variables as well, initial values must be supplied for them. These initial values are computed by multiplying and by T. The coordinates of expressed in terms of are . has the same relationship with . These last relationships fully determine the model.
The model is solved using a similar approach to that used for the 4ν t-octahedron in Section 5.3. An initial iteration is done using the penalty formulation in conjunction with Fletcher-Reeves. After this 10 iterations are done with the exact formulation in conjunction with Fletcher-Reeves to bring the values to convergence. The derivatives of the objective function with respect to the independent coordinate values are all less than . Member clearances are all greater than 0.15 model units.
Table 5.12 shows the values for the final lengths and relative forces;15 Table 5.13 shows the final values for the coordinates of the basic points, and Figure 5.11 shows the final design.
| ||||||||||||||||||||||||
|
Table 5.12: 2ν Hexagon/Triangle T-Icosahedron: Final Member Lengths and Forces |
| ||||||||||||||||
|
Table 5.13: 2ν Hexagon/Triangle T-Icosahedron: Final Coordinate Values | ||||||||||||||||
 Figure 5.11: 2ν Hexagon/Triangle T-Icosahedron: Final Design |
12 P stands for pentagon.
13 Cartesian coordinates allow to be expressed more simply as just a permutation of .
14 Derived using a formula provided in Rogers76, Chapter 3. See Section 6.2.3 for a general statement of the formula.
15 See Section 7.2 for the method of computing relative forces.