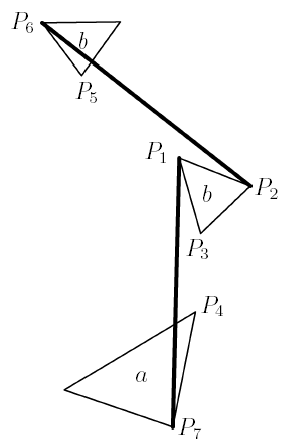
Figure 4.9: 4ν Zig-Zag T-Tetrahedron: Representative Struts
A Practical Guide to Tensegrity Design
Table of Contents
4.2 Diamond Structures
4.3 Zig-Zag Structures
4.3.1 Zig-Zag Structures: Descriptive Geometry
A zig-zag structure retains the struts and tendon triangles of the corresponding diamond structure; however, now adjacent tendon triangles are interconnected with only one tendon instead of two. This single tendon connects the "noses" of the two tendon triangles. Examination of the structure from the struts' point of view shows each strut is traversed by a "zig-zag" of three tendons. The simplest zig-zag tensegrity is the t-tetrahedron examined in Section 2.4 (Figure 2.8). Again, since more complex zig-zag structures are not amenable to the treatment used in that simple structure, the general procedure is illustrated using the zig-zag version of the 4ν t-tetrahedron examined in Section 4.2.
 Figure 4.9: 4ν Zig-Zag T-Tetrahedron: Representative Struts |
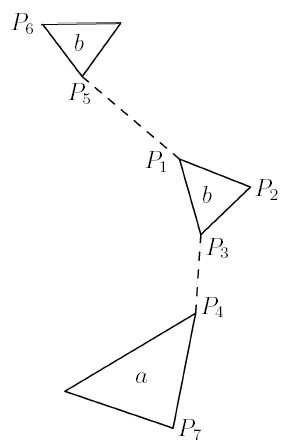 Figure 4.10: 4ν Zig-Zag T-Tetrahedron: Representative Tendons |
Figures 4.9 and 4.10 respectively show representative examples of the interconnecting struts and tendons. In these figures, the model has been expanded so that the struts are longer than in the initial geodesic calculation, while the tendon triangles remain the same size. This is done since, in the initial configuration, the noses of the tendon triangles touch each other and so the interconnecting zig-zag tendons have zero length. Expanding the structure without increasing the sizes of the tendon triangles gives the interconnecting tendons a non-zero length. The lengths of these tendons can be minimized to get a valid tensegrity. In the initial configuration, these tendons are certainly of minimum length, and the structure is theoretically a tensegrity in that configuration, but practically it isn't an interesting solution since the strut and its transformations intersect each other.
4.3.2 Zig-Zag Structures: Mathematical Model
The list of points is the same as that in Section 4.2.2, as is the list of constrained members. To avoid the problem of ending up with a solution in which the minimum of the objective is zero, the struts and are lengthened from and 0.919401 to 2 and respectively. In the objective function the diamond tendons of Section 4.2.2, , , and , are replaced by the zig-zag tendons and . As mentioned, their initial lengths are zero. Table 4.10 enumerates the end points of these additional members.
| ||||||||||||||||||||
|
Table 4.10: 4ν Zig-Zag T-Tetrahedron: Zig-Zag Tendon End Points |
The relevant mathematical programming problem becomes:
As before, only the coordinates of , , and are variables in the minimization process since the coordinates of , and are specified to be symmetry transforms of the coordinates of these points. Also, all inequality constraints are assumed to be met with equality.
4.3.3 Zig-Zag Structures: Solution
With the increased lengths of the struts, the initial values used for the problem no longer satisfy the constraints. With the best partitioning of the system (that used in Section 4.2.3), Newton's method diverges when it is applied to the system to solve the constraint equations. So, in this case, the penalty formulation is used with a penalty value of . The problem thus becomes:
Ten iterations of the method of Fletcher-Reeves are applied to this reformulated objective function. These iterations bring the constraints close enough to a solution that the penalty formulation can be discarded for the exact formulation. Another ten iterations of Fletcher-Reeves bring the system to a solution.
The final values for the lengths of members in the objective function are summarized in Table 4.11. The corresponding point values are summarized in Table 4.12.
| ||||||
|
Table 4.11: 4ν Zig-Zag T-Tetrahedron: Final Objective Member Lengths |
| ||||||||||||||||||||||||
|
Table 4.12: 4ν Zig-Zag T-Tetrahedron: Final Coordinate Values | ||||||||||||||||||||||||
The value of the objective function is 1.03848. In this structure, there is no problem with non-effective constraints as there is in the previous structure. Figure 4.11 shows the final design.
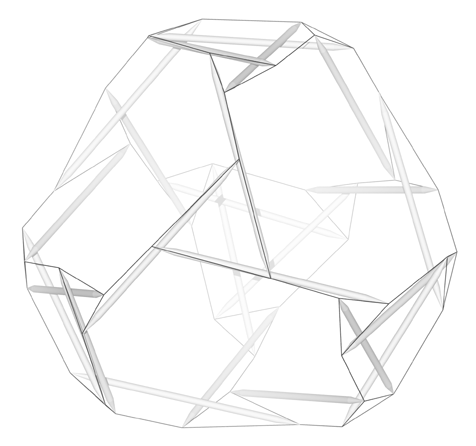 Figure 4.11: 4ν Zig-Zag T-Tetrahedron: Final Design |