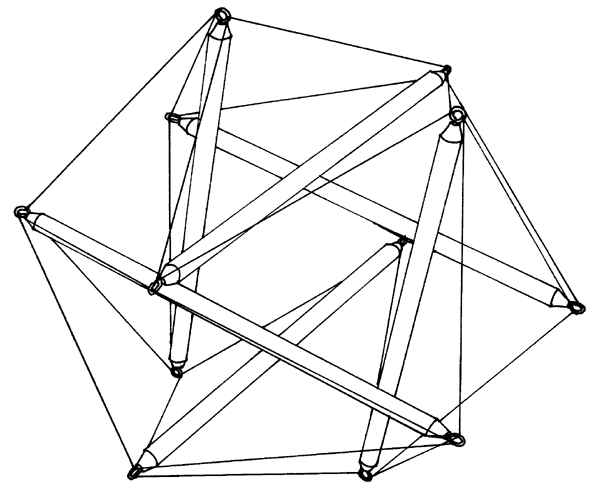
Figure 2.5: Tensegrity Icosahedron
A Practical Guide to Tensegrity Design
Table of Contents
2.2 T-Prism: The Simplest Tensegrity
2.3 T-Icosahedron: A Diamond Tensegrity
 Figure 2.5: Tensegrity Icosahedron |
The t-icosahedron is illustrated in Figure 2.5. It was first exhibited by Buckminster Fuller at Black Mountain College in 1949.13 It is one of the few tensegrities which exhibit mirror symmetry. Its network of tendons would mark out a cuboctahedron if the (non-planar) quadrilaterals in which the struts are nested were changed to squares. The struts are inserted as the diagonals of these squares so each strut is parallel to the strut in the opposite square and so no strut shares a vertex with another strut. This tensegrity is classified as a "diamond" type because each strut is surrounded by a diamond of four tendons by which it is seemingly supported by two adjacent struts. This type contrasts with the "zig-zag" type which is described in Section 2.4.
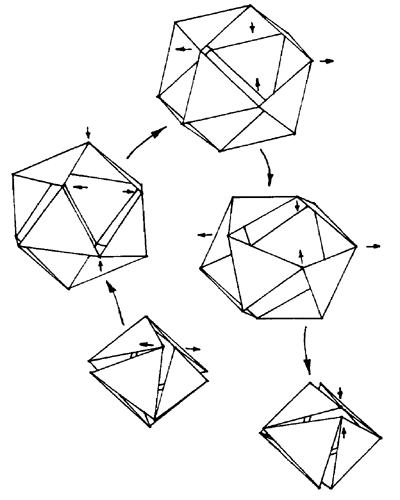 Figure 2.6: T-Icosahedron: Transformations |
Figure 2.6 shows how the system of tendons can vary from a doubled-up octahedral arrangement to a cuboctahedron and then all the way back down to an octahedron. The place where a typical strut goes is marked by a pair of small outward-pointing arrows. These small arrows also indicate the direction of movement of this pair of opposite points of the quadrilateral as the tendon system goes through its transformations. An inward-pointing pair of small arrows indicates how the other pair of points in the quadrilateral moves during the transformations.
Just past the middle of the transformations, the distance between the points indicated by the outward-pointing arrows reaches a maximum. By inserting the struts into the tendon system at this stage, the structure can be stabilized since any other stage in the transformations cannot accommodate a strut of this length. So, in the computations here, the member lengths for this structure are computed here by maximizing the length of the struts with respect to a fixed length for the tendons. This contrasts with the approach taken in Section 2.2 with the t-prism where the struts were fixed in length and the side tendons were minimized.
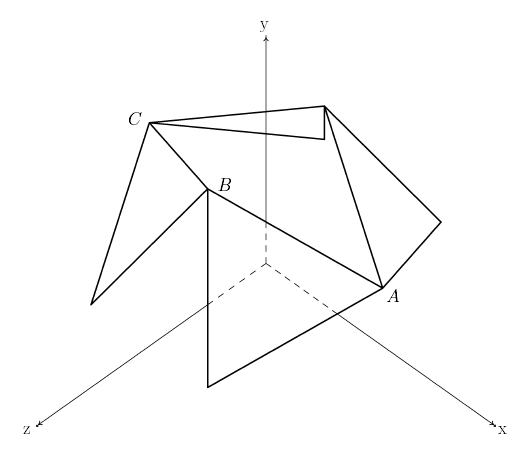 Figure 2.7: T-Icosahedron: Cartesian Coordinates |
The octahedral symmetry of the t-icosahedron gives the Cartesian coordinate system a real advantage in analyzing this structure since the Cartesian coordinate axes exhibit exactly the same symmetry. Figure 2.7 presents the model used here. For clarity, it shows only one half of the structure. It can be imagined that the xz plane has halved one of the intermediate stages from Figure 2.6 and only the half of the figure with positive y coordinates has been retained. The tendon configuration is extremely simple in that at every stage each point is symmetric to all of the others.14 So when the coordinates for one point are known, the symmetry transformations of the tensegrity can be applied to find the coordinates of any other point. In addition, the coordinate axes can be placed so that one of the coordinates is always zero.
The coincidence of the symmetry of the tensegrity with that of the coordinate system is most readily exploitable if the first point, , is chosen to lie in the positive quadrant of the plane. Its coordinates are , and . To do a mathematical analysis, two other points, and , are needed. They are used to express the equations for the length of a strut (which is being maximized) and the length of a tendon (which represents a constraint). A glance at Figure 2.6 shows that is obtained from by rotating the figure about the axis through origin and the point by .15 The corresponding rotation of the coordinate axes takes the axis into the axis, the axis into the axis and the axis into the axis. This means the coordinates of are , and . is obtained from by a rotation about the axis. So , and .
Thus, the problem can be expressed as follows:
The value for the fixed lengths of the tendons has been chosen as 1. Substituting using the standard Pythagorean length formula yields:
This problem can be solved using the method of Lagrange.16 The adjoined objective function
is differentiated by , and and the resultant equations set to zero obtaining:
|
|
The second equation says . Substituting that result into the third equation gives:
So , and the strut length is .
The Theorem of Pythagoras and the symmetry of the Cartesian coordinate system combined to make the work very easy here. Expressing points as symmetry transformations of other points can be quite a mess, the general case involving a matrix multiplication, but here a few permutations sufficed.
So working with structures with octahedral symmetry is very desirable just from a computational point of view. In later sections some spherical tensegrity trusses are studied where the use of octahedral symmetry is a practical necessity just from a geometric point of view. This being the case, computational complexities are kept to a minimum if Cartesian coordinates are used.
14 Points being symmetric to each other means that, given one point on the structure and any other point on the structure, the structure can be rotated so the given point is positioned where the other point used to be and the structure appears to be unmoved. In addition to the points, all the tendons in this model are symmetric to each other, as are all the struts.
15 This axis is not shown in the figure. If it were, it would point straight out at the viewer from the origin and thus only be visible as a point.
16 See any calculus text, for example Leithold72, pp. 951-954.