Having constructed the Revisited Concentric Five-fold Prisms, my thoughts turned to prisms with even numbers of struts. It occurred to me I might construct a prism with mirror symmetry. This would truly be something different since all the tensegrity prisms I've made so far are enantiomorphic; that is, they have left- and right-hand versions and are therefore not mirror symmetric.
So I went back to the six-fold prism and came up with the configuration seen in the photo above without the white equilateral tendon triangles at the top and the bottom. I got it into a configuration where the tendons traced the outline of the regular truncated octahedron.* Some of the edges of the truncated octahedron are missing, but the ones that are present are right where they should be.
In its mathematical formulation, it was quite a strange creature. It exhibited a valid solution at the configuration I found for it, and all the members had appropriate prestresses. However, the solution was very local and unstable, and a slight change to one of the parameters of the problem sent the solution imploding to the global solution diagrammed in the ray-trace below.
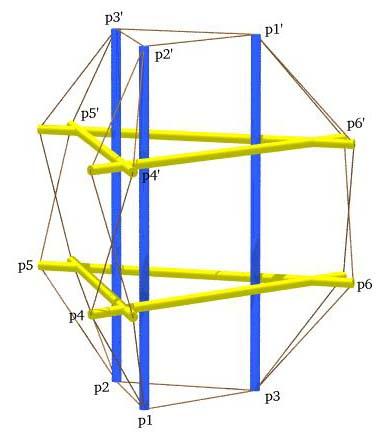
Orthogonal Girdled Six-fold Prism (Global Solution)
with Point Labels
The model I first assembled exhibited a similar instability except there appeared to be no way it could be persuaded to configure itself to the local solution I had found with my software. I went back to the drawing board and found that the mathematical solution was stabile when two equilateral tendon triangles were inserted at the ends of the prism. The solution is still local, but not so unstable.
Fortunately for my patience, which was wearing thin, the model exhibited this stability as well once these tendon triangles were inserted. I had to use the flour jar I keep the fishing line and wires in as a jig to stabilize things while I was inserting these additional tendons. Theoretically their prestress is zero, but practically they are absolutely essential for the assembly of the model.
As Quincy3 (a.k.a. Brian Quincy Hutchins) of the Geodesic listserv pointed out to me, the stabilizing tendon triangles polarize the structure's symmetry, so it's mirror image has a different form from the original structure like all the other tensegrity prisms I've worked with. I hesitate to call it enantiomorphic since which form should be called right-handed and which left-handed can only be decided arbitrarily as far as I can see.
This tensegrity represents the mental state of Posthumus at the beginning of Act V, Scene I of William Shakespeare's Cymbeline:
|
For thee, O Imogen, even for whom my life Is every breath a death, to the face of peril Myself I'll dedicate. Let me make men know More valor in me than my habits show. Gods, put the strength o' th' Leonati in me! To shame the guise o' th' world, I will begin The fashion: less without and more within. |
The white tendon triangles represent his love and lust for Imogen which keep him from imploding. I completed assembly of this study on March 10, 2004. For assembly information, see the datasheet. This model is also available on the Tensegrity Viewer as "6-Fold Ortho-Girdled Prism".