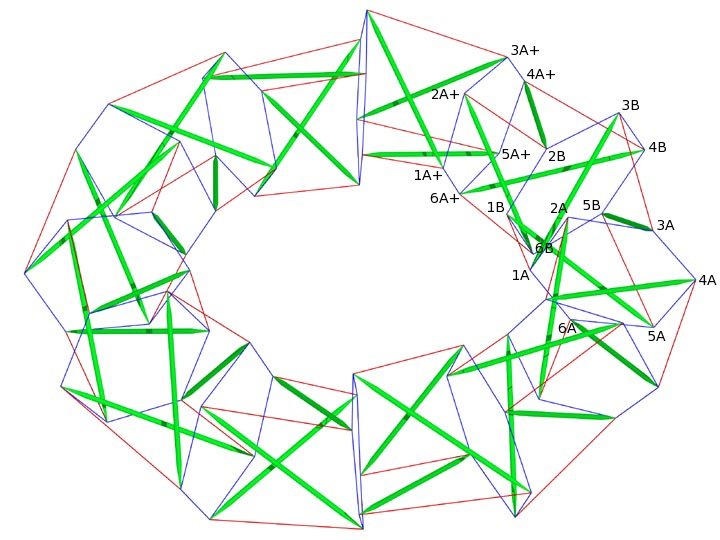
Oblique View of the Twelve-Stage Tensegrity Torus
with Point Labels
(VRML Model)
Member Descriptions
[name, end point names, weight (if in objective function),
second power of length (if a constraint), member category,
Obj/Con/Exc (put in objective function, use as a constraint or
exclude from computations), flags]
For assembly purposes, only the name and end point names are
of interest. The other information may be of interest after
A Practical Guide to Tensegrity Design has been consulted.
# struts
<Member> s13 p1A p3B -1.0 sqr(2.2) 1 Con CalcClear *
<Member> s35 p3A p5B -1.0 sqr(2.4) 1 Con CalcClear *
<Member> s51 p5A p1B -1.0 sqr(2.2) 1 Con CalcClear *
<Member> s24 p2B p4A+ -1.0 sqr(2.4) 1 Con CalcClear *
<Member> s46 p4B p6A+ -1.0 sqr(2.4) 1 Con CalcClear *
<Member> s62 p6B p2A+ -1.0 sqr(2.2) 1 Con CalcClear *
# tendons
<Member> t12A p1A p2A 1.00 1 3 Con *
<Member> t23A p2A p3A 1.00 1 3 Con *
<Member> t34A p3A p4A 1.00 1 3 Con *
<Member> t45A p4A p5A 1.00 1 3 Con *
<Member> t56A p5A p6A 1.00 1 3 Con *
<Member> t61A p6A p1A 1.00 1 3 Con *
<Member> t12B p1B p2B 1.00 1 3 Con *
<Member> t23B p2B p3B 1.00 1 3 Con *
<Member> t34B p3B p4B 1.00 1 3 Con *
<Member> t45B p4B p5B 1.00 1 3 Con *
<Member> t56B p5B p6B 1.00 1 3 Con *
<Member> t61B p6B p1B 1.00 1 3 Con *
<Member> t1AB p1A p1B 1.00 sqr(1.0) 2 Con *
<Member> t3AB p3A p3B 1.00 sqr(1.8) 2 Con *
<Member> t5AB p5A p5B 1.00 sqr(1.8) 2 Con *
<Member> t2BA p2B p2A+ 1.00 sqr(1.3) 2 Con *
<Member> t4BA p4B p4A+ 1.00 sqr(2.1) 2 Obj *
<Member> t6BA p6B p6A+ 1.00 sqr(1.3) 2 Con *
In-Situ Member Lengths
These are the lengths of the members when they are in place
and prestress is applied. The strut lengths are from
screw-eye center to screw-eye center, as are the tendon lengths.
The values are in model units.
s13: 2.2 s35: 2.4 s51: 2.2
s24: 2.4 s46: 2.4 s62: 2.2
t12A: 1 t23A: 1 t34A: 1
t45A: 1 t56A: 1 t61A: 1
t12B: 1 t23B: 1 t34B: 1
t45B: 1 t56B: 1 t61B: 1
t1AB: 1 t3AB: 1.8 t5AB: 1.8
t2BA: 1.3 t4BA: 2.00111 t6BA: 1.3
Relative Member Prestress Force Magnitudes
These values are useful for developing an assembly
strategy for the structure. The tighter tendons are much
easier to tie in place early on, while the looser tendons
can be left to the last. This information is also used
to adjust tendon lengths since the measured length of a tendon
will be shorter for a highly-stressed tendon with the same
in-situ length as a tendon which is not so stressed.
s13: -4.54304 s35: -3.04858 s51: -4.54304
s24: -3.6661 s46: -3.6661 s62: -5.58341
t12A: 4.61372 t23A: 1.83869 t34A: 2.97757
t45A: 1.40255 t56A: 3.58335 t61A: 2.40645
t12B: 2.40645 t23B: 3.58335 t34B: 1.40255
t45B: 2.97757 t56B: 1.83869 t61B: 4.61372
t1AB: 3.65567 t3AB: 2.15891 t5AB: 2.15891
t2BA: 3.11919 t4BA: 2.00111 t6BA: 3.11919
Average tendon force magnitude: 2.76987
Construction Lengths (in millimeters and halves)
The construction length of a tendon is less than the in-situ
length since when the tendon is measured off it isn't under
any prestress force. The construction length for the strut
represents the length of the 5/16-inch-diameter wooden dowel.
The tendons were made of braided nylon fishing line.
Prestress forces were assumed not to affect strut lengths.
Elongation of Tendon of Unit Cross Section
Under Force of Average Magnitude (fraction)> .02
Length Scale Factor> 238/2.4
Strut and Tendon Hub Adjustments - s;t> 4 3.5
(The 4 mm adjustment for the strut is the amount
the screw-eye center extends from the dowel. The 3.5 mm
adjustment for the tendon is half the outer diameter of the
screw eye.)
s13: 210 0 s35: 230 0 s51: 210 0 s24: 230 0
s46: 230 0 s62: 210 0 t12A: 89 0 t23A: 91 0
t34A: 90 0 t45A: 91 0 t56A: 90 0 t61A: 90 1
t12B: 90 1 t23B: 90 0 t34B: 91 0 t45B: 90 0
t56B: 91 0 t61B: 89 0 t1AB: 90 0 t3AB: 169 0
t5AB: 169 0 t2BA: 119 0 t4BA: 188 1 t6BA: 119 0

Oblique View of the Twelve-Stage Tensegrity Torus
with Point Labels
(VRML Model)
structure file: torus/x3l12torusa2.rc
variable file: torus/x3l12torusa2.dat
digit list: src/mm.dls
|
CONTACT:
Bob Burkhardt
Tensegrity Solutions
Box 426164
Cambridge, MA 02142-0021
USA
e-mail: bobwb@juno.com