Here's a skew eight-prism. I first ran into skew prisms in an article by René Motro, Sihem Belkacem and Nicolas Vassart. (See their skew three-prism that I built.) Recently I deduced that these can be designed fairly simply using non-linear optimization techniques. For me, the defining characteristics of a skew prism are that the points of both ends fall in two parallel planes, and that a perpendicular line through the center of one end does not pass through the center of the other end.
This construction harkens back to a style I used early in my tensegrity model-building career, but haven't used again until now. See the Tensegrity Vector Equilibrium for an early example of this style. For this construction, I took time to paint the struts. The tendons are made of 12-pound-test braided nylon fishing line, a little lighter than the 25-pound-test line I use when building with 5/16-inch-diameter (8 mm) struts. The lighter line seemed appropriate for these 3/16-inch-diameter (4.75 mm) struts.
The datasheet was completed March 25, 2005, and I completed the model on April 26, 2005. The design goes against the grain of a lot of my previous work since all the struts have different lengths, but I'm fascinated by the skewness, even more so after building this model. These prisms could find application where cantilevered structures are desirable.
The base of the model is equilateral, while the cap is not. The non-equilateralness is minor and can be hard to notice. The non-equilateral cap distorts the equilateral base so it doesn't outline a regular octagon. Below is a design for the prism with both ends equilateral. With both ends equilateral, the ends also align themselves into regular octagons. This is true whether or not the two end polygons are of equal size. In addition, the prestress in all the tendons composing a polygon are equal, something I didn't expect in a skewed structure.
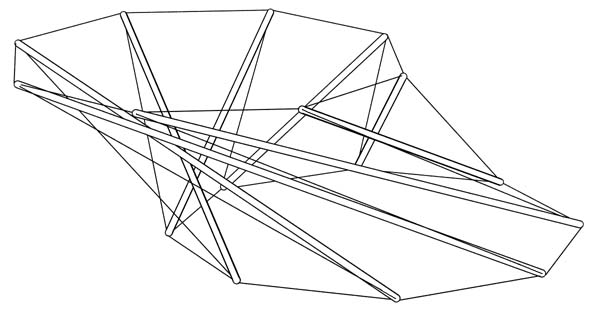
The second design with its regular octagonal ends is also available on the Tensegrity Viewer as "Skew Eight-Prism". VRML models are available for both the design with the non-regular octagonal ends and the one with the regular octagonal ends. The paper outlining my methodology for designing skew tensegrity prisms is also available.
An article of interest here is Milenko Masic, Robert E. Skelton, Philip E. Gill, "Algebraic tensegrity form-finding", International Journal of Solids and Structures, Vol. 42, Nos. 16-17 (Aug 2005), pp. 4833-4858. It shows that tensegrity equilibrium is preserved by affine transformations (a linear transformation plus a translation). This covers skew transformations as well as many other interesting ones. The result allows a variety of interesting variations from an initial tensegrity design to be easily explored. For a prism with non-equilateral ends, my methodology is useful for getting an initial design. A skew transform can then be applied to generate different amounts of or directions of skewness or even a non-skew prism with irregular ends.