On October 27, 2003, three months after writing up my unsuccessful attempt to duplicate the "skew 4-prismatic system" from the Motro et al. paper cited in the Skew Three-Prism slide, I tried again to duplicate the computations. I didn't succeed completely, but I think I came closer this time.
I started by disregarding "Fig. 6 Squew 4-prismatic system" from the Motro et al. paper, thus discarding the 2-fold symmetry for a completely asymmetric structure. I put the two long struts adjacent to each other, the two short struts adjacent to each other, and gave the tendons at the base of the prism length 1.0. I used Motro et al.'s lengths for the struts and apex tendons, but custom-computed the lengths of the side tendons by minimizing the sum of second powers of their lengths subject to the other member lengths.
The resulting side tendon lengths were nowhere near the values Motro et al. gave, but the structure exhibited a skewness very similar to what the "skew 3-prismatic system" exhibited with the apex and base tendons falling in parallel planes. This asymmetric skewness is very different from the symmetric structure exhibited by Motro et al. in their Fig. 6 and better fits in with what was done before for the "skew 3-prismatic system".
Again I assemble my values and Motro et al.'s values in a table for comparison. As before, my figures are in bold face. For a completely successful duplication of Motro et al.'s results, the figures in the "Stress" (Motro et al.) and "Member force" (my values) columns should be proportional, and the side tendon lengths should coincide, which didn't happen. However, everything else matches. In addition, all the member forces in the apex tendons are equal, as are all the member forces in the base tendons. Given the asymmetry of the structure, this is not something I would expect, but matches Motro et al.'s results.
Just as surprising is the way the member forces of the struts are equal to their lengths. Given the way I computed the structure, this was to be expected for the side tendons, but seeing it in the struts as well was a surprise. And surprising as well is the way the apex points and the base points align into planes. Given the asymmetry of the structure, this was not to be expected. All these surprises in addition to the other matches give me some confidence that I've duplicated something essential from Motro et al.'s model.
(Note: Motro et al.'s figures follow the European custom of using a comma instead of a decimal point. In addition, the endpoints of members 7(c) and 8(c) have been swapped as have the endpoints of members 10(s) and 11(s) in comparison to the table in the Four-fold Reduced-Symmetry Prism slide.)
| Member | End points | Force density |
Length (Motro et al.) | Length (me) |
Stress | Member force |
|---|---|---|---|---|---|---|
| 1(c) | 1 - 2 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 2(c) | 2 - 3 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 3(c) | 3 - 4 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 4(c) | 4 - 1 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 5(c) | 2 - 6 | 1 | 1,118 | 1.70044 | 1,118 t | 1.70044 |
| 6(c) | 1 - 5 | 1,5 | 1,718 | 2.05273 | 2,577 t | 2.05273 |
| 7(c) | 3 - 7 | 1 | 1,118 | 1.34839 | 1,118 t | 1.34839 |
| 8(c) | 4 - 8 | 1,5 | 1,718 | 1.77210 | 2,577 t | 1.77210 |
| 9(s) | 2 - 5 | -1,5 | 2,516 | 2.516 | -3,774 t | -2.516 |
| 10(s) | 4 - 7 | -1 | 1,5 | 1.5 | -1,5 t | -1.5 |
| 11(s) | 1 - 8 | -1,5 | 2,516 | 2.516 | -3,774 t | -2.516 |
| 12(s) | 3 - 6 | -1 | 1,5 | 1.5 | -1,5 t | -1.5 |
| 13(c) | 5 - 6 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 14(c) | 6 - 7 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 15(c) | 7 - 8 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 16(c) | 8 - 5 | ? | 1.0? | 1.0 | ? | 0.63710 |
All results considered, I can only conclude something got garbled between the computations and writing them up in the Motro et al. paper, at least for the "skew 4-prismatic system". The structure almost exhibits 2-fold symmetry on at least one axis through its side. The photo below shows that.

After experimentation I found that there was a family of skew four-prisms I could generate. I could choose a length for two adjacent struts, another different length for the other two struts, a length for the four tendons at one end of the prism, a length for the four tendons at the other end of the prism (possibly the same as the previous length -- in this case, the structure becomes symmetric with the two-fold symmetry axis alluded to in the photo above) and finally choose the side tendon lengths so the sum of their second powers is minimized subject to the other lengths. A skew prism always obtains.
This was also what I did with the skew three-prism. I went on to try the technique for a five- and a six-prism, but it didn't seem to work very well. The prisms were skew, but the ends were non-planar. A year and a half later, when I was writing this up for possible publication in the Journal of the IASS, I found a simple procedure that allows skew prisms of all orders to be computed. For an example, see Skew Eight-Prism.
So here it is February 13, 2006. In my skew-prism paper, I've refined my method. It turns out there are even more ways to generate a skew 4-prism with the Motro et al. strut lengths, almost. In the following approach, I keep the two "long" struts opposite each other and constrain only one of the short struts. The sum of second powers of the side tendon lengths are minimized, but now the additive inverse of the second power of the length of the remaining "short" strut figures into the objective function. In this configuration, the "short" strut expands to dwarf all the rest of the struts and tendons. The following table summarizes the results, again with the values from Motro et al. available for comparison. The end points for members 7(c), 8(c), 10(s) and 11(s) have changed.
| Member | End points | Force density |
Length (Motro et al.) | Length (me) |
Stress | Member force |
|---|---|---|---|---|---|---|
| 1(c) | 1 - 2 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 2(c) | 2 - 3 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 3(c) | 3 - 4 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 4(c) | 4 - 1 | 1 | 0,901 | 0.901 | 0,901 t | 0.70711 |
| 5(c) | 2 - 6 | 1 | 1,118 | 2.52552 | 1,118 t | 2.52552 |
| 6(c) | 1 - 5 | 1,5 | 1,718 | 1.99567 | 2,577 t | 1.99567 |
| 7(c) | 4 - 8 | 1 | 1,118 | 1.93232 | 1,118 t | 1.93232 |
| 8(c) | 3 - 7 | 1,5 | 1,718 | 2.47576 | 2,577 t | 2.47576 |
| 9(s) | 2 - 5 | -1,5 | 2,516 | 2.516 | -3,774 t | -2.516 |
| 10(s) | 1 - 8 | -1 | 1,5 | 1.5 | -1,5 t | -1.5 |
| 11(s) | 4 - 7 | -1,5 | 2,516 | 2.516 | -3,774 t | -2.516 |
| 12(s) | 3 - 6 | -1 | 1,5 | 3.22653 | -1,5 t | -3.22653 |
| 13(c) | 5 - 6 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 14(c) | 6 - 7 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 15(c) | 7 - 8 | ? | 1.0? | 1.0 | ? | 0.63710 |
| 16(c) | 8 - 5 | ? | 1.0? | 1.0 | ? | 0.63710 |
And here's a raytrace of the new configuration:
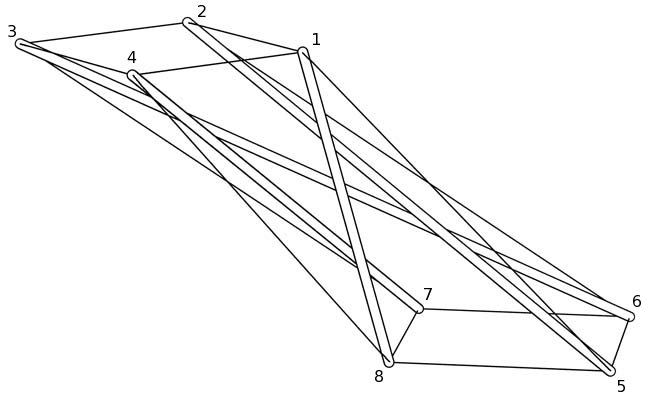
This doesn't do much better as a match for the original Motro et al. prism, but I thought it was interesting as a demonstration that the previous method wasn't the only way of generating a skew 4-prism with two strut lengths equal. It turns out that tensegrity prisms don't lose their tensegrity properties when skewed along their central axes; so, there's quite a variety of ways to generate a skew prism. For example, a skew 4-prism with four different strut lengths is possible.
A skew prism is completely determined by specifying lengths for any three of its side members. In specifying the minimization problem for the prism, those three side members, along with the end tendons, go in the constraints. The rest of the side members go into the objective function: side tendons get a weight of 1.0; struts get a weight of -1.0. The ends don't have to be equilateral. This is true for prisms of all orders. This methodology also provides a way to study prisms with non-equilateral ends, and it seems likely that simple algebraic formulas can be worked out to describe all these prisms.
An article of interest here is Milenko Masic, Robert E. Skelton, Philip E. Gill, "Algebraic tensegrity form-finding", International Journal of Solids and Structures, Vol. 42, Nos. 16-17 (Aug 2005), pp. 4833-4858. It shows that tensegrity equilibrium is preserved by affine transformations (a linear transformation plus a translation). This covers skew transformations as well as many other interesting ones. The result allows a variety of interesting variations from an initial tensegrity design to be easily explored. For a prism with non-equilateral ends, my method is useful for getting an initial design. A skew transform can then be applied to generate different amounts of or directions of skewness or even a non-skew prism with irregular ends.
So, I still think something got garbled in the tables of the original Motro et al. paper. I recently found a paper by Motro (René Motro, "Structural Morphology of Tensegrity Systems", International Journal of Space Structures, Vol. 11, Nos. 1 & 2, pp. 233-240.) which puts the skew 4-prism structure into perspective. It is meant to be part of an array of prisms (see Figures 10, 11 and 12 from the paper cited). That array is a class 4 tensegrity structure, that is, up to four struts can meet at a node. I'll have to see what I can do with that at some point.