On March 17, 1997, I tried duplicating the computations for a "skew 3-prismatic system" which was presented in a paper I'd found. The paper was René Motro, Sihem Belkacem and Nicolas Vassart, "Form Finding Numerical Methods for Tensegrity Systems", p. 711 in John F. Abel, John W. Leonard, and Celina U. Penalba eds., Spatial, lattice and tension structures, proceedings of the IASS-ASCE International Symposium 1994 held in conjunction with the ASCE Structures Congress XII, April 24-29, 1994, Georgia World Congress, Atlanta, Georgia, USA. Kind of a mouthful, and worth every syllable. Those proceedings had a lot of interesting papers for the tensegrity aficionado.
This paper was especially interesting for me because of the example it presented with the member lengths and even stresses (what I call member forces) tabulated. Everything checked out. Just recently (July 17, 2003), I went back to the model and revised it for my latest tensegrity software. It is such an unusual tensegrity, I thought I'd build a model of it and give it a wider audience. The photo makes it look like it's defying gravity, but I actually took the photo on the side of a roof.
After handling this model and thinking about it some time, I realized it reminded me of the polyhedron composed of three triple-bonded tetrahedra which is the building block of the tetrahelix. With that in mind, I tweaked the model so the two long struts were of identical length and all the tendons and short strut were of length one. I got something that almost looks the same.

The new version of the skew 3-prism varies slightly from the tetrahelix building block in that the two virtual edges (2 - 6 and 3 - 4) are slightly longer than one (1.11106). I'll include a table of the member statistics mostly because of an odd symmetry I found: members 4(c) and 6(c) have the same member force as 1(c) and 10(c). I would expect 1(c) and 10(c) to have the same force and 4(c) and 6(c) to have the same force because they are symmetrical, but the match between the two groups is a surprise. Note the large member force in the backbone of the module, 5(c). The magnitude of the member force matches the length for members 7(s) and 8(s) just because of the way I scaled things. The member forces are relative values and could be scaled by any positive constant.
| Member | End points | Length | Member force |
|---|---|---|---|
| 1(c) | 1 - 2 | 1.0 | 0.738566 |
| 2(c) | 2 - 3 | 1.0 | 0.32827 |
| 3(c) | 3 - 1 | 1.0 | 0.54548 |
| 4(c) | 1 - 6 | 1.0 | 0.738566 |
| 5(c) | 2 - 4 | 1.0 | 1.44447 |
| 6(c) | 3 - 5 | 1.0 | 0.738566 |
| 7(s) | 1 - 4 | 1.63681 | -1.63681 |
| 8(s) | 2 - 5 | 1.63681 | -1.63681 |
| 9(s) | 3 - 6 | 1.0 | -0.787929 |
| 10(c) | 4 - 5 | 1.0 | 0.738566 |
| 11(c) | 5 - 6 | 1.0 | 0.54548 |
| 12(c) | 6 - 4 | 1.0 | 0.32827 |
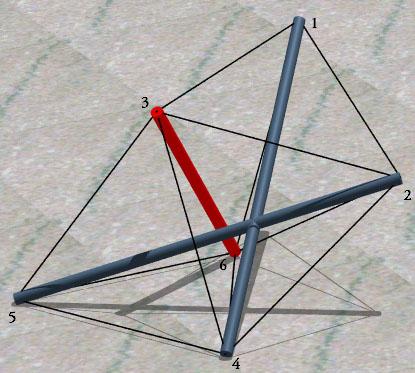
This wasn't enough for you, as your eye has strayed over the above figure and this text. In the above figure, the two "virtual" (imaginary?) tendons have been made real (see 13(c) and 14(c) in the table below), and both have been constrained to have length one. With all that triangulation, it's not a difficult tensegrity to compute. The two long blue struts now intersect. I didn't bother with a model since my usual dowel-and-fishing-line approach isn't very feasible. Instead I used POV-Ray to render the picture above. The member statistics (note all the rational numbers, and the lengths of 7(s) and 8(s) would be rational as well if we were looking at second powers):
| Member | End points | Length | Member force |
|---|---|---|---|
| 1(c) | 1 - 2 | 1.0 | 0.666667 |
| 2(c) | 2 - 3 | 1.0 | 0.222222 |
| 3(c) | 3 - 1 | 1.0 | 0.666667 |
| 4(c) | 1 - 6 | 1.0 | 0.666667 |
| 5(c) | 2 - 4 | 1.0 | 1.33333 |
| 6(c) | 3 - 5 | 1.0 | 0.666667 |
| 7(s) | 1 - 4 | 1.63299 | -1.63299 |
| 8(s) | 2 - 5 | 1.63299 | -1.63299 |
| 9(s) | 3 - 6 | 1.0 | -0.888889 |
| 10(c) | 4 - 5 | 1.0 | 0.666667 |
| 11(c) | 5 - 6 | 1.0 | 0.666667 |
| 12(c) | 6 - 4 | 1.0 | 0.222222 |
| 13(c) | 3 - 4 | 1.0 | 0.222222 |
| 14(c) | 2 - 6 | 1.0 | 0.222222 |
The end-point labels were inserted in the last two figures using Microsoft Paint. The floor tile in the last figure came from the classical section of the Museum of Fine Arts, Boston. It belongs more to the infrastructure than the collection, like I doubt it has an accession number.
As randome inventor Dick Fischbeck pointed out to me, all these structures are reminiscent of Kenneth Snelson's X-Module.