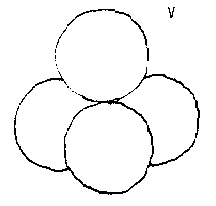
| Previous Section | Contents | Next Section |
The two volumes of Synergetics disclose my discovery and definition of systems and structural systems in a mathematically elegant hierarchy of primitive, pre-time and -size self-inter-structuring systems of minimum complexity, topologically involving only the first four prime numbers, 1, 2, 3, 5 in respect to Euler's three essential visual aspects of the topology of all polyhedra -- Vertexes, Faces, and Edges.
Euler showed that the relative abundance of Vs, Fs, and Es in all "polyhedra" will always be V + F = E + 2. For instance, in an octahedron, six Vertexes plus eight Faces equals twelve Edges plus two. In a tetrahedron, four Vertexes plus four Faces equals six Edges plus two. In the rhombic dodecahedron fourteen vertices plus twelve faces equal twenty four edges plus two; in a cube eight vertices plus six faces equal twelve edges plus two.
On the following page you will find my chart of the hierarchy of topological characteristics (primitive, pre-time and -size) of structural systems, in which table what has been called the cube is discovered to be the combined positive and negative tetrahedra with their combined four vertexes each producing the eight vertexes constituting the "cube" (without the cube's twelve edges). When the twelve-edges cube is formed as a necklaced tube structure, it spontaneously collapses having no triangles to stabilize it.
In this same table, you will find that when the tetrahedron's volume is taken as unity that the tetra-cube's overall vertex-defined volume is exactly three and the octahedron's volume is exactly four and the all-space-filling rhombic dodecahedron volume is exactly six.
| Table 1 | Synergetics Hierarchy of Topological Characteristics of Omnitriangulated Polyhedral Systems |
| (Table 223.64 from Synergetics) |
I now return to Euler's topology and to my own always and only experientially -- operationally -- developed reconsideration of Euler's premises. All of my work began with nature's minimum structural system which, based on the tetrahedron's superficially defined four planes of symmetry is always four dimensional. There is no experimentally demonstrable, independent two dimensionality in Universe. There are only impenetrably high frequency-of-event surfaces of systems. Euler along with all other mathematicians and physicists erred in assuming that the paper or blackboard on which they demonstrated their geometry had only a two-dimensional surface and was not a substance having an insideness and outsideness.
There is a multi-millenia precedent for playing mathematical games in which the player makes believe that he has, for instance, a surface of nothing which nonetheless has a wavy shape (despite that shape can be accomplished only by physical "somethings" systems). Such mathematical games cannot be realistically identified as science, which gas Jeans so correctly stated is, "concerned with setting in order the facts of experience." Science is concerned with learning how Universe (nature) operates. Synergetics is mathematical science. It is pursued only experientially. Professor Percival Bridgman of Harvard discovered that what made possible Einstein's breakthrough was his insistence on treating not only with physically demonstrable facts but also with all the systemically relevant physical facts demonstrably affecting the central measurements. Bridgman called this Einstein's "operational procedures." Synergetic mathematics is always concerned with whole systems and not with parts. Parts are nonexistent independent of systems.
I have to observe that this sheet of paper on which I am writing has substance, an insideness, and a continuous surface rounding at the paper's edges to become the other side of the paper on which I can also write. This piece of paper is a system dividing Universe into a macro-outsideness and a micro-withinness. Experience begins with whole systems. We do not have parts until we have systems. Systems are always four dimensional or more.
I have also to observe that if I take four unit-radius spheres, they will most closely pack together as the tetrahedron since each of a tetrahedron's four corner balls represent Euler's four vertexes (V).
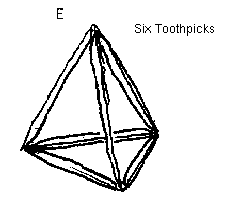
I also observe that if I take six toothpicks, I can glue their twelve ends together in collections of three per vertex to make a tetrahedron whose structure is provided almost exclusively by Euler's Edges (E).
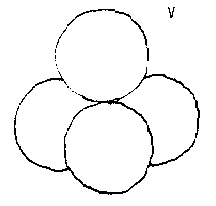
| 
|
| Tetrahedron Shown by Vertexes | Tetrahedron Shown by Lines |
[Editor's note: The above two in-text figures and the next three in-text figures appear as neater mechanical drawings in Fig. 6.13 of Cosmography.]
Again I observe that if I take an equilateral triangle of paper I can bisect the edges of that triangle and fold its three corners together bending the paper along the three connecting lines between the bisected edges of th triangle thus to form a tetrahedron whose visibility is provided almost exclusively by Euler's Faces (F).
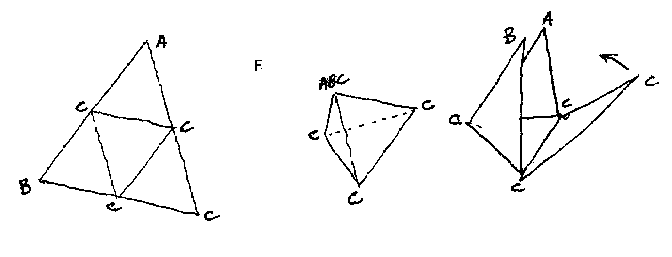
Tetrahedra Shown by Faces
We next realize that these faces -- which the Greeks called hedra (sides; polyhedra, many sides) -- are not necessary to the structuring of the simplest tetrahedron. To the Greeks who used carved out marble to demonstrate "solid" geometry, the multi-sides (faces, facets) seemed obviously solid, e.g. Plato's five "solids," which were the tetrahedron, cube, octahedron, icosahedron, and pentagonal dodecahedron.
I next observe that the six toothpicks did give us a very satisfactory visual awareness of the tetrahedron without any faces. I then discover that I can have four clouds in the sky, one outwardly in the sky from three others which describe a tetrahedron without sides or faces and without the six visible interrelationship lines of the four event loci that describe the corners of the minimum system -- the tetrahedron whose four clouds are indeed held apart at specific distances by atmospheric and other forces. Therefore, the minimum description of our awareness recognition of such a minimum system's existence should not be a tetrahedron but a tetra-vertexion.
Now realizing the primary necessity of four vertex event loci in defining a four-vertexion (for instance, the four puffy clouds) we realize that we could speak of these "something" events as the loci of complex micro-systems in-four-different-directions from the observer -- "four somethings having six pairs of induced, invisible, congruent, non-substantial, most economical, interrepulsive, and interattractive interrelationship lines."
The six induced, most economical interrelationship lines frame four windows through which we view nothingness, emptiness. Through the four triangularly framed windows of the tetrahedron, we look through the nothingness (emptiness) into the microcosmic withinness nothingness (emptiness) which is the for the moment, untuned-in, micro-frequency irrelevant events -- while from inside the tetrahedron we look out through the triangular windows' nothingness at the macrocosmic withoutness nothingness -- the presently untuned-in macro-irrelevancies.
We find then the topological law of systems is that the number of somethings plus the number of empty nothingness windows equals the number of system interrelationships plus two as a more accurate use of Euler's topological aspects. S = number of somethings (systems) and N = number of nothingness (empty) windows and R = number of lines of interrelationships between all the system's somethings. The four somethings defining systems are of necessity systems themselves not at the moment differentially tunable. They are static "squeaks" (systems).
Euler's basic topological formula is now experientially expressed as S + N = R + 2 (e.g., 4 + 4 = 6 + 2 for a tetrahedron). Four somethings plus four nothings equal six relationships plus the number two.
We next acknowledge the experientially demonstrated fact that all independent system in Universe have a least resistant axis of spinnability. Every such axis has two poles. We now acknowledge that two of our four system identifying somethings (which means too of the tetrahedron's four corners) as having the function of spin-axis poles of any independent system. We can now say inventorily that four somethings, minus two somethings serving as poles, plus four nothings equals six edges: i.e., S - P + N - R. This is Euler's formula in its most omni-experience-considerate state, 2PS + (2S + 4N = 6R).
| Previous Section | Contents | Next Section |